题目内容
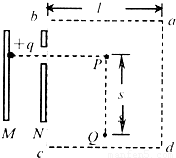
 如图所示,无初速度带正电粒子经过MN两平行板间的电场加速后,从N板小孔射出,当粒子到达P点时,宽度l=1.6m的长方形abcd区域内出现太小B=0.4T、方向垂直纸面且随时间交替变化的磁场,每经T0=
如图所示,无初速度带正电粒子经过MN两平行板间的电场加速后,从N板小孔射出,当粒子到达P点时,宽度l=1.6m的长方形abcd区域内出现太小B=0.4T、方向垂直纸面且随时间交替变化的磁场,每经T0=| π |
| 4 |
| q |
| m |
(1)加速电压为200V时,求带电粒子经过N板小孔时的速度大小;
(2)带电粒子能否经过Q点?
(3)若带电粒子能经过Q点,则加速电压的最大值应是多少?
分析:(1)加速电压为200V时,由动能定理求出速度.
(2)带电粒子进入磁场后由洛伦兹力提供向心力,根据牛顿第二定律,推导出周期公式,分析粒子运动的周期与磁场变化周期的关系,由半径来确定能否经过Q点;
(3)根据长度的关系,来确定相碰条件,从而求得最小半径,由半径公式与动能定理,共同求出加速电压最大值.
(2)带电粒子进入磁场后由洛伦兹力提供向心力,根据牛顿第二定律,推导出周期公式,分析粒子运动的周期与磁场变化周期的关系,由半径来确定能否经过Q点;
(3)根据长度的关系,来确定相碰条件,从而求得最小半径,由半径公式与动能定理,共同求出加速电压最大值.
解答:解:(1)带电粒子在加速电场中,由动能定理得:qU=
mv2
解得:v=
代入数据解得:v=2×103m/s
(2)粒子以速度v匀速运动到P点时,出现垂直纸面向外的匀强磁场,粒子向下偏转做匀速圆周运动,
周期:T=
=
×10-3s
则:T=2T0
粒子在磁场中做匀速圆周运动,有qvB=m
,
则得 半径r=
=0.5m
则r<
=0.8m故粒子恰做完半圈圆周运动时磁场改变方向,继续做新的半圆周运动,由于PQ=s=3m,2r=1m,所以带电粒子能经过Q点.粒子的运动轨迹如图所示.
(3)粒子在磁场中运动的半径可表示为r=
=
,要使带电粒子能经过Q点,除保持磁场变化周期不变外,还需满足:
①r≤
;即
≤
,
化简得 U≤
=512V
②s=2Nr;即N=
,
解得 U=
当N=1时,U=1800V,不满足要求;
当N=2时,电压U最大,Umax=450V
答:
(1)加速电压为200V时,带电粒子经过N板小孔时的速度大小为2×103m/s;
(2)带电粒子能经过Q点.
(3)若带电粒子能经过Q点,则加速电压的最大值应是450V.
| 1 |
| 2 |
解得:v=
|

代入数据解得:v=2×103m/s
(2)粒子以速度v匀速运动到P点时,出现垂直纸面向外的匀强磁场,粒子向下偏转做匀速圆周运动,
周期:T=
| 2πm |
| qB |
| π |
| 2 |
则:T=2T0
粒子在磁场中做匀速圆周运动,有qvB=m
| v2 |
| r |
则得 半径r=
| mv |
| qB |
则r<
| l |
| 2 |
(3)粒子在磁场中运动的半径可表示为r=
| mv |
| qB |
| 1 |
| B |
|
①r≤
| l |
| 2 |
| 1 |
| B |
|
| l |
| 2 |
化简得 U≤
| B2l2q |
| 8m |
②s=2Nr;即N=
| Bs |
| 2 |
|
解得 U=
| 1800 |
| N2 |
当N=1时,U=1800V,不满足要求;
当N=2时,电压U最大,Umax=450V
答:
(1)加速电压为200V时,带电粒子经过N板小孔时的速度大小为2×103m/s;
(2)带电粒子能经过Q点.
(3)若带电粒子能经过Q点,则加速电压的最大值应是450V.
点评:考查粒子在磁场中做匀速圆周运动,由洛伦兹力提供向心力,根据牛顿第二定律,推导出的半径与周期公式,并掌握动能定理在此应用,同时还掌握几何关系的运用.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 (2012?湖南模拟)如图所示,A、B均为半个绝缘正方体,质量均为m,在A、B内部各嵌入一个带电小球,A带电量为+q,B带电量为-q,且两个小球的球心连线垂直于AB接触面.A、B最初靠在竖直的粗糙墙上.空间有水平向右的匀强电场,场强大小为E,重力加速度为g.现将A、B无初速度释放,下落过程中始终相对静止,忽略空气阻力,则下列说法中正确的是( )
(2012?湖南模拟)如图所示,A、B均为半个绝缘正方体,质量均为m,在A、B内部各嵌入一个带电小球,A带电量为+q,B带电量为-q,且两个小球的球心连线垂直于AB接触面.A、B最初靠在竖直的粗糙墙上.空间有水平向右的匀强电场,场强大小为E,重力加速度为g.现将A、B无初速度释放,下落过程中始终相对静止,忽略空气阻力,则下列说法中正确的是( ) 如图所示,L1、L2为平行的两个磁场边界线,L1上方和L2下方都是垂直纸面向里的磁感应强度大小相同的匀强磁场,L1、L2之间无磁场;A、B是边界L2上相距一定距离的两点.带电粒子从A点以初速度v0与L2成30°角斜向上射出,经过偏转后正好能经过B点,不计粒子重力.下列说法中正确的是( )
如图所示,L1、L2为平行的两个磁场边界线,L1上方和L2下方都是垂直纸面向里的磁感应强度大小相同的匀强磁场,L1、L2之间无磁场;A、B是边界L2上相距一定距离的两点.带电粒子从A点以初速度v0与L2成30°角斜向上射出,经过偏转后正好能经过B点,不计粒子重力.下列说法中正确的是( ) 如图所示,水平两块带电金属板a、b正对放置,在板间形成匀强电场,电场方向竖直向上.板间同时存在与电场正交的匀强磁场,假设电场、磁场只存在于两板间的空间区域.一束电子以一定的初速度v0从两板的左端中央,沿垂直于电场、磁场的方向射入场中,无偏转的通过场区.已知板长为 l,两板间距为d,两板问电势差为U,电子所带电荷量为e,其质量为m,不计电子所受重力和电子之间的相互作用力.
如图所示,水平两块带电金属板a、b正对放置,在板间形成匀强电场,电场方向竖直向上.板间同时存在与电场正交的匀强磁场,假设电场、磁场只存在于两板间的空间区域.一束电子以一定的初速度v0从两板的左端中央,沿垂直于电场、磁场的方向射入场中,无偏转的通过场区.已知板长为 l,两板间距为d,两板问电势差为U,电子所带电荷量为e,其质量为m,不计电子所受重力和电子之间的相互作用力.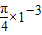 ,磁场方向变化一次,粒子刚到P点时磁场方向垂直纸面向外.已知P点正下方有一点Q,P、Q之间的距离s=3m,PQ是ab和cd的垂直平分线,带电粒子的比荷
,磁场方向变化一次,粒子刚到P点时磁场方向垂直纸面向外.已知P点正下方有一点Q,P、Q之间的距离s=3m,PQ是ab和cd的垂直平分线,带电粒子的比荷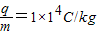 ,重力可忽略不计.问:
,重力可忽略不计.问: