题目内容
14.以初速度v0水平抛出的物体,当水平方向的分位移与竖直方向的分位移相等时( )| A. | 运动的时间t=$\frac{2{v}_{0}}{g}$ | B. | 瞬时速率vt=$\sqrt{5}$v0 | ||
| C. | 水平分速度与竖直分速度大小相等 | D. | 位移大小等于$\frac{2\sqrt{2}{{v}_{0}}^{2}}{g}$ |
分析 平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,抓住水平位移和竖直位移相等求出运动的时间,结合速度时间公式判断水平分速度和竖直分速度的关系,根据平行四边形定则求出瞬时速度的大小.通过水平位移和竖直位移,根据平行四边形定则求出位移的大小.
解答 解:A、根据题意有:$\frac{1}{2}$gt2=v0t,得:t=$\frac{2{v}_{0}}{g}$,故A正确.
BC、竖直分速度为:vy=gt=2v0≠v0.瞬时速率vt=$\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}$=$\sqrt{5}{v}_{0}$,故B正确,C错误.
D、水平位移x=v0t=$\frac{2{v}_{0}^{2}}{g}$,根据平行四边形定则知,位移大小为:s=$\sqrt{2}$x=$\frac{2\sqrt{2}{v}_{0}^{2}}{g}$.故D正确.
故选:ABD.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解.

练习册系列答案
相关题目
4. 在直角坐标系xOy中,x轴上方有磁感应强度为B的匀强磁场,在x轴下方有电场强度为E的匀强电场.从M点以一定的初速度水平射出一带正电粒子(不计重力)恰好经坐标原点O到达N,如图所示,已知M点的横坐标为-a,且MN两点关于坐标原点对称,粒子经O点时速度恰好与水平方向成45°角,则下列说法正确的是( )
在直角坐标系xOy中,x轴上方有磁感应强度为B的匀强磁场,在x轴下方有电场强度为E的匀强电场.从M点以一定的初速度水平射出一带正电粒子(不计重力)恰好经坐标原点O到达N,如图所示,已知M点的横坐标为-a,且MN两点关于坐标原点对称,粒子经O点时速度恰好与水平方向成45°角,则下列说法正确的是( )
 在直角坐标系xOy中,x轴上方有磁感应强度为B的匀强磁场,在x轴下方有电场强度为E的匀强电场.从M点以一定的初速度水平射出一带正电粒子(不计重力)恰好经坐标原点O到达N,如图所示,已知M点的横坐标为-a,且MN两点关于坐标原点对称,粒子经O点时速度恰好与水平方向成45°角,则下列说法正确的是( )
在直角坐标系xOy中,x轴上方有磁感应强度为B的匀强磁场,在x轴下方有电场强度为E的匀强电场.从M点以一定的初速度水平射出一带正电粒子(不计重力)恰好经坐标原点O到达N,如图所示,已知M点的横坐标为-a,且MN两点关于坐标原点对称,粒子经O点时速度恰好与水平方向成45°角,则下列说法正确的是( )| A. | 粒子从M运动到O的时间与从O运动到N的时间相等 | |
| B. | 粒子在磁场中的轨道半径为$\sqrt{2}$a | |
| C. | M点的纵坐标为($\sqrt{2}$-1)a | |
| D. | 粒子到达N点时的速度恰好水平 |
5.下列说法正确的是( )
| A. | 因为功有正负,所以功是矢量 | |
| B. | 功的大小只由力和位移决定 | |
| C. | 把重1N的物体匀速举高1m,克服重力做功为-1J | |
| D. | 做功的过程就是物体能量的转化过程 |
4.一条船在静水中的速度为4m/s,它要横渡一条40m宽的河,水流速度为3m/s,下列说法正确的是( )
| A. | 船过河的位移一定大于40m | B. | 船无法垂直到达对岸 | ||
| C. | 船过河的最短时间为10s | D. | 船过河的最短位移为40m |
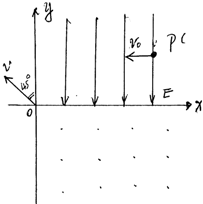 如图所示,xy平面的第一象限内有沿负y方向的匀强电场,在第四象限内有垂直于纸面向外的匀强磁场,现有一质量为m,电量+q的粒子,以初速度v0沿负x方向坐标为(3l,l)的P点开始运动,接着进入磁场后从原点射出,射出的速度方向与y轴正方向夹角为45°,不计粒子重力,求:
如图所示,xy平面的第一象限内有沿负y方向的匀强电场,在第四象限内有垂直于纸面向外的匀强磁场,现有一质量为m,电量+q的粒子,以初速度v0沿负x方向坐标为(3l,l)的P点开始运动,接着进入磁场后从原点射出,射出的速度方向与y轴正方向夹角为45°,不计粒子重力,求:
 有一个正方形线框的线圈匝数为10匝,边长为20cm,线框总电阻为1Ω,线框绕OO′轴以10πrad/s的角速度匀速转动,如图,垂直于线框平面向里的匀强磁场的磁感应强度为0.5T,求:
有一个正方形线框的线圈匝数为10匝,边长为20cm,线框总电阻为1Ω,线框绕OO′轴以10πrad/s的角速度匀速转动,如图,垂直于线框平面向里的匀强磁场的磁感应强度为0.5T,求: 如图所示,均匀介质中两波源S1、S2分别位于x轴上x1=0、x2=14m处,质点P位于x轴上xP=4m处,t=0时刻两波源同时开始由平衡位置向y轴正方向振动,振动周期均为T=0.1s,传播速度均为v=40m/s,波源S1S2的振幅均为A=2cm,则
如图所示,均匀介质中两波源S1、S2分别位于x轴上x1=0、x2=14m处,质点P位于x轴上xP=4m处,t=0时刻两波源同时开始由平衡位置向y轴正方向振动,振动周期均为T=0.1s,传播速度均为v=40m/s,波源S1S2的振幅均为A=2cm,则 如图所示,电路中的灯泡标有“0.1V,0.4W”,电源的电动势为4V,内阻为0.05Ω,电动机内阻为0.1Ω,此时灯泡与电动机都正常工作求:
如图所示,电路中的灯泡标有“0.1V,0.4W”,电源的电动势为4V,内阻为0.05Ω,电动机内阻为0.1Ω,此时灯泡与电动机都正常工作求: