题目内容
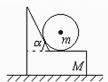
 如图所示,一块带有斜面和平台的木块,质量为M,斜面与水平方向倾角为α,木块置于水平面上,与水平面间的摩擦系数是μ(μ>tga).将一个质量为m的光滑球放在平台上,并与斜面相靠,当球与木块一起在图示平面内沿水平方向相对于地面运动(速度不为零)时,在木块上施加的水平力F的大小范围是( )
如图所示,一块带有斜面和平台的木块,质量为M,斜面与水平方向倾角为α,木块置于水平面上,与水平面间的摩擦系数是μ(μ>tga).将一个质量为m的光滑球放在平台上,并与斜面相靠,当球与木块一起在图示平面内沿水平方向相对于地面运动(速度不为零)时,在木块上施加的水平力F的大小范围是( )分析:M与m具有相同的加速度,抓住m的临界加速度方向水平向右,结合牛顿第二定律求出推力F的范围.
解答:解:A、当F的方向向右,临界情况是球对平台的压力为零,受重力和斜面的弹力,根据平行四边形定则知,球的合力为mgtanα,则临界加速度a=gtanθ,对整体分析,根据牛顿第二定律得,F-μ(M+m)g=(M+m)a,解得最大推力Fm=(M+m)g(μ+tanα),对整体分析,知物体要向右运动,则F≥μ(M+m)g,则μ(m+M)g≤F≤(m+M)g(μ+tga).故A正确,B错误.
C、若F的方向向左,球和木块保持相对静止,知整体的加速度方向向右,整体做匀减速直线运动,同理,可知临界加速度a=gtanθ,对整体分析,有:μ(M+m)g-F=(M+m)a,解得最小推力Fmin=(m+M)g(μ-tana),则推力大小为μ(m+M)g≥F≥(m+M)g(μ-tana).故C正确,D错误.
故选AC.
C、若F的方向向左,球和木块保持相对静止,知整体的加速度方向向右,整体做匀减速直线运动,同理,可知临界加速度a=gtanθ,对整体分析,有:μ(M+m)g-F=(M+m)a,解得最小推力Fmin=(m+M)g(μ-tana),则推力大小为μ(m+M)g≥F≥(m+M)g(μ-tana).故C正确,D错误.
故选AC.
点评:解决本题的关键知道两物体具有相同的加速度,通过小球求出临界加速度,从而根据牛顿第二定律进行求解.

练习册系列答案
相关题目
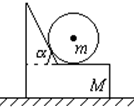 如图所示,一块带有斜面和平台的木块,质量为M,斜面与水平方向倾角为α,木块置于水平面上,与水平面间的摩擦系数是μ(μ>tga).将一个质量为m的光滑球放在平台上,并与斜面相靠,当球与木块一起在图示平面内沿水平方向相对于地面运动(速度不为零)时,在木块上施加的水平力F的大小范围是
如图所示,一块带有斜面和平台的木块,质量为M,斜面与水平方向倾角为α,木块置于水平面上,与水平面间的摩擦系数是μ(μ>tga).将一个质量为m的光滑球放在平台上,并与斜面相靠,当球与木块一起在图示平面内沿水平方向相对于地面运动(速度不为零)时,在木块上施加的水平力F的大小范围是