题目内容
如图所示，某人通过一定滑轮吊起质量为m的物体，开始时绳子与水平方向的夹角为60°，当人将重物匀速提起，人由A点水平方向运动xAB=l到B点时，绳与水平方向成30°，在这一过程中，下列说法正确的是：（重力加速度为g）（ ）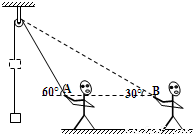
A．人对绳的拉力做功mgl
B．人对绳的拉力做功
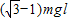
C．人沿水平方向也应作匀速直线运动
D．人沿水平方向运动的速度越来越小
【答案】分析：根据功能关系，人做的功等于系统机械能的增加量；将人的速度沿着平行绳子和垂直绳子方向正交分解，沿着绳子方向的分速度等于重物的速度．
解答：解：A、B、设A点与滑轮的悬挂点的高度差为h，根据几何关系，AB间距为：
l=htan60°-htan30° ①
重物上升的高度为：
H=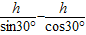
②
联立解得
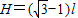
根据功能关系，人做的功等于系统机械能的增加量，故W=mgH=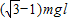
，故A错误，B正确；
C、D、将人的速度沿着平行绳子和垂直绳子方向正交分解，如图
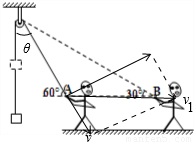
人的速度为：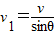
，由于角度θ不断增加，故人的速度不断减小，故C错误，D正确；
故选BD．
点评：本题关键是根据功能关系求解变力的功，同时要结合运动的合成与分解进行分析，不难．
解答：解：A、B、设A点与滑轮的悬挂点的高度差为h，根据几何关系，AB间距为：
l=htan60°-htan30° ①
重物上升的高度为：
H=
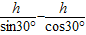②联立解得
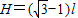
根据功能关系，人做的功等于系统机械能的增加量，故W=mgH=
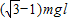，故A错误，B正确；C、D、将人的速度沿着平行绳子和垂直绳子方向正交分解，如图
人的速度为：
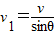，由于角度θ不断增加，故人的速度不断减小，故C错误，D正确；故选BD．
点评：本题关键是根据功能关系求解变力的功，同时要结合运动的合成与分解进行分析，不难．
练习册系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
如图所示，某人通过一根跨过定滑轮的轻绳提升一个质量为m的重物，开始时人在滑轮的正下方，绳下端A点离滑轮的距离为H．人由静止拉着绳向右移动，当绳下端到B点位置时，人的速度为v，绳与水平面夹角为θ．问在这个过程中，人对重物做了多少功？
m(vcosθ)2
