题目内容
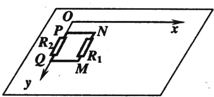 如图所示,空间存在一个方向垂直桌面向下的磁场.现将质量为m、边长为L的正方形线框MNPQ,静止放在光滑绝缘足够大的水平桌面上,PQ边与y轴重合.MN边的电阻为R1,PQ边的电阻为R2,线框其余部分电阻不计.
如图所示,空间存在一个方向垂直桌面向下的磁场.现将质量为m、边长为L的正方形线框MNPQ,静止放在光滑绝缘足够大的水平桌面上,PQ边与y轴重合.MN边的电阻为R1,PQ边的电阻为R2,线框其余部分电阻不计.(1)若磁场随时间的变化规律为Bt=B0+kt(k为大于零的已知常数),求线框中感应电流的大小和方向.
(2)若磁场不随时间变化,而是按照下列情况分布:磁感应强度沿y轴方向均匀分布,沿x轴方向按规律Bx=kx变化(k为大于零的已知常数),线框从t=0时刻、以初速度ν0由图示位置向x轴正方向平动.求在图示位置线框所受安培力的大小和方向.
(3)在第(2)问中,若R1=2R2,求在整个运动过程中,电阻R1产生的焦耳热.
分析:1、由电动势的定义式求电动势,由楞次定律判断电流方向;
2、先计算出感应电动势和感应电流,再由安培力公式求安培力;
3、由动能定理或能量关系求产生的热量.
2、先计算出感应电动势和感应电流,再由安培力公式求安培力;
3、由动能定理或能量关系求产生的热量.
解答:解:(1)根据法拉第电磁感应定律可知:E=
=L2
=kL2
感应电流的大小为:I=
=
感应电流的方向沿NPQMN.
(2)MN处的磁感应强度为kL,所以MN切割产生的电动势为:E=BLv0=kL2v0,
PQ处磁感应强度为0,所以其产生的电动势也为0,
因此线框中的感应电动势为:E=kL2v0
线框中的感应电流为:I=
=
线框受的安培力方向沿-x方向(或水平向左)
安培力大小为:F=LIB=
(3)线框最终停止,根据能量关系,线框中产生的焦耳热为:Q=
m
电阻R1产生的焦耳热为:QR1=
Q=
m
答:(1)线框中感应电流的大小为
,感应电流的方向沿NPQMN.
(2)在图示位置线框所受安培力的大小为
,线框受的安培力方向沿-x方向.
(3)在整个运动过程中,电阻R1产生的焦耳热为
m
.
| △Φ |
| △t |
| △B |
| △t |
感应电流的大小为:I=
| E |
| R1+R2 |
| kL2 |
| R1+R2 |
感应电流的方向沿NPQMN.
(2)MN处的磁感应强度为kL,所以MN切割产生的电动势为:E=BLv0=kL2v0,
PQ处磁感应强度为0,所以其产生的电动势也为0,
因此线框中的感应电动势为:E=kL2v0
线框中的感应电流为:I=
| E |
| R1+R2 |
| kL2v0 |
| R1+R2 |
线框受的安培力方向沿-x方向(或水平向左)
安培力大小为:F=LIB=
| k2L4v0 |
| R1+R2 |
(3)线框最终停止,根据能量关系,线框中产生的焦耳热为:Q=
| 1 |
| 2 |
| v | 2 0 |
电阻R1产生的焦耳热为:QR1=
| R1 |
| R1+R2 |
| 1 |
| 3 |
| v | 2 0 |
答:(1)线框中感应电流的大小为
| kL2 |
| R1+R2 |
(2)在图示位置线框所受安培力的大小为
| k2L4v0 |
| R1+R2 |
(3)在整个运动过程中,电阻R1产生的焦耳热为
| 1 |
| 3 |
| v | 2 0 |
点评:本题是道综合性较强的题目,运用了法拉第电磁感应定律,动能定理等知识点,要细心阅读题目,仔细计算.

练习册系列答案
相关题目
 如图所示,空间存在一方向竖直向下的匀强电场.长L=0.5m的绝缘细线一端固定于电场中的O点,另一端系一带电荷量q=+4×10-5C、质量m=0.1kg的小球在竖直平面内做圆周运动已知当小球以速率v=4m/s通过最高点A时,绝缘细线中的张力为2N,求匀强电场的场强大小(取g=10m/s2)
如图所示,空间存在一方向竖直向下的匀强电场.长L=0.5m的绝缘细线一端固定于电场中的O点,另一端系一带电荷量q=+4×10-5C、质量m=0.1kg的小球在竖直平面内做圆周运动已知当小球以速率v=4m/s通过最高点A时,绝缘细线中的张力为2N,求匀强电场的场强大小(取g=10m/s2) (2007?朝阳区二模)如图所示的空间存在一匀强磁场,其方向为垂直于纸面向里,磁场的右边界为MN,在MN右侧有一矩形金属线圈abcd,ab边与MN重合.现使线圈以ab边为轴按图示方向匀速转动,将a、b两端连到示波器的输入端,若电流从a 到b为正,则从下图中示波器观察到的ab中电流随时间变化的规律是( )
(2007?朝阳区二模)如图所示的空间存在一匀强磁场,其方向为垂直于纸面向里,磁场的右边界为MN,在MN右侧有一矩形金属线圈abcd,ab边与MN重合.现使线圈以ab边为轴按图示方向匀速转动,将a、b两端连到示波器的输入端,若电流从a 到b为正,则从下图中示波器观察到的ab中电流随时间变化的规律是( ) (2011?长沙县模拟)如图所示的空间存在一匀强磁场,其方向为垂直于纸面向里,磁场的右边界为MN,在MN右侧有一矩形金属线圈学abcd,ab边与MN重合.现使线圈以ab边为轴按图示方向匀速转动,从cd边刚好进入磁场开始计时,则ab中电流随时间变化的规律是( )
(2011?长沙县模拟)如图所示的空间存在一匀强磁场,其方向为垂直于纸面向里,磁场的右边界为MN,在MN右侧有一矩形金属线圈学abcd,ab边与MN重合.现使线圈以ab边为轴按图示方向匀速转动,从cd边刚好进入磁场开始计时,则ab中电流随时间变化的规律是( ) 如图所示的空间存在一匀强磁场,其方向为垂直于纸面向里,磁场的右边界为MN,在MN右侧有一矩形线圈abcd,ab边与MN重合.线圈在外力作用下以ab边为轴按图示方向匀速转动,规定电流从a→b→c→d→a为正方向,则下列图象能正确表示线圈中电流随时间变化的规律是( )
如图所示的空间存在一匀强磁场,其方向为垂直于纸面向里,磁场的右边界为MN,在MN右侧有一矩形线圈abcd,ab边与MN重合.线圈在外力作用下以ab边为轴按图示方向匀速转动,规定电流从a→b→c→d→a为正方向,则下列图象能正确表示线圈中电流随时间变化的规律是( )



