题目内容
如图如示,分布在半径为r的圆形区域内的匀强磁场,磁感应强度为B,方向垂直纸面向里,电荷量为q、质量为m的带正电的粒子从磁场边缘a点沿圆的半径aO方向射入磁场,离开磁场时速度方向偏转了60°角.试确定:
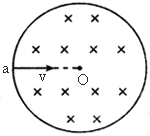
(1)粒子做圆周运动的半径;
(2)粒子的入射速度;
(3)若保持粒子的速率不变,从a点入射时速度的方向顺时针转过60°角,粒子在磁场中运动的时间.
答案:略
解析:
解析:
|
答案:(1) 思路点拨:设带正电粒子从磁场边缘 c点射出,则射出方向的反向延长线经过磁场圆心O,如图所示,作aO与cO的垂线,两垂线相交于 , , 即为粒子在磁场区域中运动的轨迹的圆心,再利用几何关系即可求出轨迹半径. 即为粒子在磁场区域中运动的轨迹的圆心,再利用几何关系即可求出轨迹半径.
正确解答: (1)设粒子从磁场边缘c点射出,则出射速度沿Oc方向,设轨迹圆心为 ,由题意可知 ,由题意可知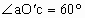 , ,
粒子轨道半径为: (2) 由洛伦兹力公式和牛顿第二定律可得:
(3) 如果整个空间都充满了方向垂直于纸面向里的磁场,粒子在纸面上做圆周运动,设粒子运动一周的时间为T,则粒子在磁场中运动时间为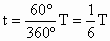 ,将 ,将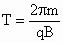 代入得: 代入得:小结点评:此类问题的特点是:所涉及磁场的边界是圆,一般要研究粒子在磁场中运动的时间,粒子能飞出磁场的条件,粒子在磁场中运动的偏转角等问题,解决的基本方法就是确定圆心,并利用几何关系,求粒子运动的半径. |

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
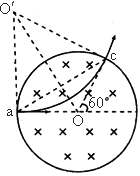
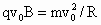
 如图所示,分布在半径为r的圆形区域内的匀强磁场,磁感应强度为B,方向垂直纸面向里.电荷量为q、质量为m的带正电粒子从磁场边缘a点处沿圆的半径AO方向射入磁场,离开磁场时速度方向偏转了60°角,试求:
如图所示,分布在半径为r的圆形区域内的匀强磁场,磁感应强度为B,方向垂直纸面向里.电荷量为q、质量为m的带正电粒子从磁场边缘a点处沿圆的半径AO方向射入磁场,离开磁场时速度方向偏转了60°角,试求: 如图所示,分布在半径为r的圆形区域内的匀强磁场,磁感应强度为B,方向垂直纸面向里.电荷量为+q、质量为m的带电粒子从磁场边缘A点沿圆半径AO方向射入磁场,粒子离开磁场时速度方向偏转了60?角.求:
如图所示,分布在半径为r的圆形区域内的匀强磁场,磁感应强度为B,方向垂直纸面向里.电荷量为+q、质量为m的带电粒子从磁场边缘A点沿圆半径AO方向射入磁场,粒子离开磁场时速度方向偏转了60?角.求: