题目内容
有一辆汽车质量为800kg，行驶在圆弧半径为50m的拱形桥面上．求：
（1）当汽车在拱顶处速度为5m/s时，拱桥对汽车的支持力．
（2）汽车以多大的速度经过拱顶时对桥恰好没有压力而腾空？（取g=10m/s2）
（1）当汽车在拱顶处速度为5m/s时，拱桥对汽车的支持力．
（2）汽车以多大的速度经过拱顶时对桥恰好没有压力而腾空？（取g=10m/s2）
分析：（1）汽车在桥顶时，重力和支持力的合力提供圆周运动的向心力，根据牛顿第二定律求出拱桥对汽车的支持力．
（2）当汽车对桥顶恰好无压力时，重力提供向心力，根据牛顿牛顿第二定律求出汽车的速度．
（2）当汽车对桥顶恰好无压力时，重力提供向心力，根据牛顿牛顿第二定律求出汽车的速度．
解答：解：（1）根据牛顿第二定律得，
mg-N=m
解得N=mg-m
=8000-800×
N=7600N．
答：拱桥对汽车的支持力为7600N．
（2）当压力为零时，有：mg=m
解得v0=
=
m/s=22.4m/s．
答：当汽车的速度为22.4m/s时，汽车对桥恰好没有压力而腾空．
mg-N=m
| v2 |
| R |
解得N=mg-m
| v2 |
| R |
| 25 |
| 50 |
答：拱桥对汽车的支持力为7600N．
（2）当压力为零时，有：mg=m
| v02 |
| R |
解得v0=
| gR |
| 500 |
答：当汽车的速度为22.4m/s时，汽车对桥恰好没有压力而腾空．
点评：解决本题的关键搞清向心力的来源，运用牛顿第二定律求解．
练习册系列答案
相关题目
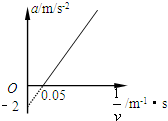（2011?河东区一模）（1）一辆汽车在平直的公路上以某一初速度运动，运动过程中保持恒定的牵引功率，其加速度a和速度的倒数（1/v）图象如图所示．若已知汽车的质量为m=1.5×103kg，则汽车运行时的功率为
