题目内容
 如图所示,两个水平摩擦轮A和B传动时不打滑,半径RA=2RB,A为主动轮.当A匀速转动时,在A轮边缘处放置的小木块恰能与A轮相对静止.若将小木块放在B轮上,为让其与轮保持相对静止,则木块离B轮转轴的最大距离为(已知同一物体在两轮上受到的最大静摩擦相等)( )
如图所示,两个水平摩擦轮A和B传动时不打滑,半径RA=2RB,A为主动轮.当A匀速转动时,在A轮边缘处放置的小木块恰能与A轮相对静止.若将小木块放在B轮上,为让其与轮保持相对静止,则木块离B轮转轴的最大距离为(已知同一物体在两轮上受到的最大静摩擦相等)( )分析:摩擦传动时,两轮边缘上线速度大小相等,摩擦力提供向心力展开讨论即可.
解答:解:摩擦传动不打滑时,两轮边缘上线速度大小相等,根据题意有:两轮边缘上有:
RAωA=RBωB
所以:ωB=
ωA
因为同一物体在两轮上受到的最大摩擦力相等,根据题意有,在B轮上的转动半径最大为r:则根据最大静摩擦力等于向心力有:
mRAωA2=mr
得:r=
=
=
故选B.
RAωA=RBωB
所以:ωB=
| RA |
| RB |
因为同一物体在两轮上受到的最大摩擦力相等,根据题意有,在B轮上的转动半径最大为r:则根据最大静摩擦力等于向心力有:
mRAωA2=mr
| ω | 2 B |
得:r=
RA
| ||
(
|
| ||
| RA |
| RB |
| 2 |
故选B.
点评:摩擦传动时,两轮边缘上线速度大小相等,抓住最大摩擦力相等是解决本题的关键.

练习册系列答案
相关题目
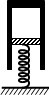 ,弹簧一端固定于水平面上,另一端与质量为m的活塞拴接在一起,开口向下、质量为M的气缸与活塞一起封闭了一定质量的气体.气缸和活塞均可与外界进行热交换.若外界环境的温度缓慢降低,则封闭气体的体积将
,弹簧一端固定于水平面上,另一端与质量为m的活塞拴接在一起,开口向下、质量为M的气缸与活塞一起封闭了一定质量的气体.气缸和活塞均可与外界进行热交换.若外界环境的温度缓慢降低,则封闭气体的体积将
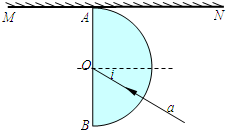
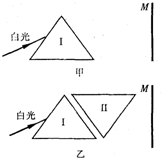 A、屏M自上而下分布的色光的波长由小到大
A、屏M自上而下分布的色光的波长由小到大
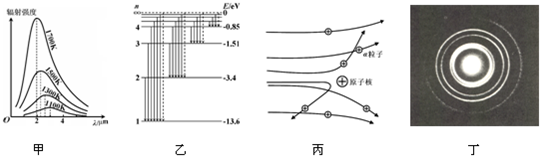

 A.
A.