题目内容
卫星在某圆形轨道上运行的速率为v，周期为T，若轨道半径增大为原来的两倍，卫星的速率变为 ，周期变为 ．
【答案】分析：根据卫星做匀速圆周运动时万有引力提供向心力公式表示出速率和周期即可求解；
解答：解：根据卫星做匀速圆周运动时万有引力提供向心力得：
F=G
=
=
得：
v=
T=2
运行轨道半径变为原来的两倍，则它受到的向心力将变为原来的四分之一，即为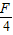
，
运行轨道半径变为原来的两倍，则
v′=
=
T′=2
=2
T
故答案为：
，2
T
点评：本题主要考查了万有引力提供向心力公式的直接应用，难度不大，属于基础题．
解答：解：根据卫星做匀速圆周运动时万有引力提供向心力得：
F=G
==得：v=
T=2
运行轨道半径变为原来的两倍，则它受到的向心力将变为原来的四分之一，即为
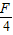，运行轨道半径变为原来的两倍，则
v′=
=T′=2
=2T故答案为：
，2T点评：本题主要考查了万有引力提供向心力公式的直接应用，难度不大，属于基础题．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目