Question

如图4-2-16所示，竖直平面上有一光滑绝缘半圆轨道，处于水平方向且与轨道平面平行的匀强电场中，轨道两端点A、C高度相同，轨道的半径为R.一个质量为m的带正电的小球从槽右端的A处无初速沿轨道下滑，滑到最低点B时对槽底压力为2mg，求小球在滑动过程中的最大速度.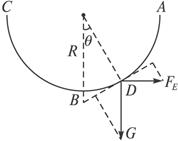

图4-2-16

两位同学是这样求出小球的最大速度的：

甲同学：B是轨道的最低点，小球过B点时速度最大，小球运动过程机械能守恒，mgR=mv²,解得小球在滑动过程中的最大速度为v=.

乙同学：B是轨道的最低点，小球过B点时速度最大，小球在B点受到轨道的支持力为N=2mg.由牛顿第二定律有F_N-mg=m，解得球在滑动过程中的最大速度为v=.

请分别指出甲、乙同学的分析是否正确，若有错，将最主要的错误指出来，解出正确的答案，并说明电场的方向.

Answer 1

思路点拨：需要强调的是物体做圆周运动的切线方向合力为零时，速度大小不再变化，在沿半径方向的合力全部提供向心力，此时一般称为物体在最低点时速度最大，但本题中由于还有电场的影响，则物体的最低点不在B点，应在切线方向合力为零处.但由小球到B点小球的支持力和重力提供向心力可求出速度，从A到B的运动过程中由动能定理可求出电场力和重力的关系，由切线方向的合外力为零确定其位置，再由动能定理求出到达该位置处的速度.

解析：甲同学的分析是错误的，乙同学的分析也是错误的.正确解法如下：

小球在滑动过程中的最大速度的位置不在最低点B.

小球在B点时：F_N-mg=m

F_N=2mg  v²=gR

从A到B，设电场力做功W_E，由动能定理W_E+mgR=mv²

得W_E=-mgR

电场力做负功，带电小球受电场力方向向右F_E==mg

电场强度方向向右

从A到B之间一定有位置D是小球运动速度方向瞬时合力为零处，也是小球速度最大处.

设OD连线与竖直方向夹角为θ,F_Ecosθ=Gsinθ

mv_m²=mgRcosθ-F_E(R-Rsinθ)

v_m=.

答案：