Question

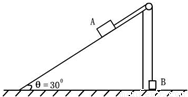
如图所示．某固定斜面倾角为30°，斜面足够长，顶上有一定滑轮．跨过定滑轮的细绳两端分别与物体A、B连接，A质量为4kg，B质量为1kg．开始时，将B按在地上不动，然后放开手，让A沿斜面下滑而B上升．所有摩擦忽略不计．当A沿斜面下滑5m后，细绳突然断了．求：物块B上升的最大高度．（设B不与定滑轮相碰，g=10m/s²）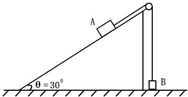

Answer 1

A沿斜面下滑5m时，A下降的高度为   
h_A=5×sin30°=2.5m；B上升的高度为         
 h_B=5m
以A为对象，由动能定理得：
mAghA-FL=

1

2

mAVB2
同理：以B为对象       
 FL-mBgL=

1

2

mBVB2
联解得   VB=2

5

m．s-1
设B再上升h′时，速度为零，由动能定理

-mBgh′=0- 1 2 mB v 2B →h′=1m

B上升的最大高度为：h=h_B+h′=5+1=6m．
答：物块B上升的最大高度为6m．