题目内容
(2004?广州二模)一束光从真空射到折射率为
的某种玻璃的表面,用i表示入射角,r表示折射角,则( )
| 2 |
分析:根据折射定律求出折射角的大小.发生全反射的条件:一从光密介质进入光疏介质,二是入射角大于等于临界角.
解答:解:A、当r=30°时,由n=
得,sini=nsinr=
,则i=45°.故A正确.
B、当入射角是90°时,根据n=
,则r=45°,可见最大的折射角是45°,所以无论入射角i是多大,折射角r都不会超过45°.故B正确.
C、因为光是从空气进入玻璃,不可能发生全反射.所以当i>45°时,光线仍有光线射入到玻璃中.故C错误.
D、假设反射光线跟折射光线恰好互相垂直,设入射角为i,折射角为β,则有i+β=90°,则得n=
=
=tani.所以i=arctan
.故D正确.
故选ABD.
| sini |
| sinr |
| ||
| 2 |
B、当入射角是90°时,根据n=
| sin90° |
| sinr |
C、因为光是从空气进入玻璃,不可能发生全反射.所以当i>45°时,光线仍有光线射入到玻璃中.故C错误.
D、假设反射光线跟折射光线恰好互相垂直,设入射角为i,折射角为β,则有i+β=90°,则得n=
| sini |
| sinβ |
| sini |
| sin(90°-i) |
| 2 |
故选ABD.
点评:解决本题的关键掌握折射定律,以及掌握全反射的条件.

练习册系列答案
相关题目
 (2004?广州二模)“二分频”音箱内有两个不同口径的扬声器,它们的固有频率分别处于高音、低音频段,分别称为高音扬声器和低音扬声器,音箱要将扩音机送来的含有不同频率的混合音频电流按高、低频段分离出来,送往相应的扬声器,以便使电流所携带的音频信息按原比例还原成高、低频的机械振动图为音箱的电路图,高、低频混合电流由a、b输入,L1和L2是线圈,C1和C2是电容器( )
(2004?广州二模)“二分频”音箱内有两个不同口径的扬声器,它们的固有频率分别处于高音、低音频段,分别称为高音扬声器和低音扬声器,音箱要将扩音机送来的含有不同频率的混合音频电流按高、低频段分离出来,送往相应的扬声器,以便使电流所携带的音频信息按原比例还原成高、低频的机械振动图为音箱的电路图,高、低频混合电流由a、b输入,L1和L2是线圈,C1和C2是电容器( ) (2004?广州二模)如图所示,绝缘光滑的半圆轨道位于竖直平面内,并处于竖直向下的匀强电场中,在轨道的上缘有一个质量为m,带电荷量为+q的小球,由静止开始沿轨道运动.下列说法正确的是( )
(2004?广州二模)如图所示,绝缘光滑的半圆轨道位于竖直平面内,并处于竖直向下的匀强电场中,在轨道的上缘有一个质量为m,带电荷量为+q的小球,由静止开始沿轨道运动.下列说法正确的是( )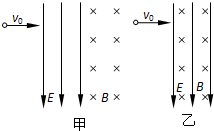 (2004?广州二模)一重力不计的带电粒子一初速度v0先后穿过宽度相同且紧邻在一起的有明显边界的匀强电场E和匀强磁场B,如图甲所示,电场和磁场对粒子总共做功W1;若把电场和磁场正交叠加,如图乙所示,粒子仍以v0的初速度穿过叠加场区对粒子总共做功W2,比较W1、W2的绝对值大小( )
(2004?广州二模)一重力不计的带电粒子一初速度v0先后穿过宽度相同且紧邻在一起的有明显边界的匀强电场E和匀强磁场B,如图甲所示,电场和磁场对粒子总共做功W1;若把电场和磁场正交叠加,如图乙所示,粒子仍以v0的初速度穿过叠加场区对粒子总共做功W2,比较W1、W2的绝对值大小( )