��Ŀ����
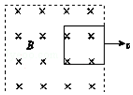
10�� ������������������Ĺ۵���������Ҳ�����ö����������ȹ۵��������ͽ��ͣ� ��ͼ��ʾ���㹻����ƽ�й⻬��������ˮƽ���ã�������ΪL��һ��������ֵΪR�ĵ��裮�������ڿռ������ֱ���µ���ǿ�ų����Ÿ�Ӧǿ��ΪB������Ϊm������Ϊr�ĵ����MN���ڵ����ϣ��䳤��ǡ�õ��ڵ����࣬�뵼��Ӵ����ã���֪�����MN�Գ��ٶ�v0�����˶���
������������������Ĺ۵���������Ҳ�����ö����������ȹ۵��������ͽ��ͣ� ��ͼ��ʾ���㹻����ƽ�й⻬��������ˮƽ���ã�������ΪL��һ��������ֵΪR�ĵ��裮�������ڿռ������ֱ���µ���ǿ�ų����Ÿ�Ӧǿ��ΪB������Ϊm������Ϊr�ĵ����MN���ڵ����ϣ��䳤��ǡ�õ��ڵ����࣬�뵼��Ӵ����ã���֪�����MN�Գ��ٶ�v0�����˶�����1����������˶����ٶ�Ϊv0ʱ��������ٶ�a�Ĵ�С��
��2��������ڵ������˶���λ��x��
��3���ӵ���������˶���ʼ��ʱ���������嶯����λ�Ʊ仯��ͼ��˵�����ɣ�
��4���ӵ���������˶���ʼ��ʱ�����Ի������嶯����λ�Ʊ仯��ͼ��˵�����ɣ�
���� ��1���ȸ��ݵ�����и�Ÿ��������Ӧ�������ڸ���ţ�ٵڶ����ɾͿ���������ٶ�a��
��2���Ե�����ļ��ٹ��̸��ݶ���������ʽ�������иʽ���ƽ����Ӧ�綯�ƣ�����ŷķ�������ƽ����Ӧ���������ݰ�������ʽ���ƽ�����������룻
��3�����ݶ��������õ�������λ�ƹ�ϵ����ʽ�����嶯����λ�Ʊ仯��ͼ��
��4�����ݶ��ܶ�����ʽ�õ�������λ��x�Ĺ�ϵʽ��ͬʱ����ȷͼ���ϵ�����ߵ�б�ʵ����壮
��� �⣺��1�������ٶ�Ϊv0ʱ�и�Ÿ��߲�����Ӧ�綯�ƣ�E=BLv1��
�����е���ǿ�ȣ�I=$\frac{E}{R+r}$��
�����ܵ���������F��=BIL��
��ţ�ٵڶ����ɣ�F��=ma��
���ԣ�a=$\frac{{B}^{2}{L}^{2}{v}_{0}}{m��R+r��}$��
��2��������Ϊ�������ɶ���������-B$\overline{I}$L•t=0-mv0��
�����е�ƽ����Ӧ������$\overline{I}$=$\frac{BL\overline{v}}{R+r}$��
�����λ�ƣ�x=$\overline{v}$t��
�����ã�$x=\frac{m{v}_{0}��R+r��}{{B}^{2}{L}^{2}}$��
��3������Ķ�����λ�ƵĹ�ϵ��$m{v}_{0}-P��=\frac{{B}^{2}{L}^{2}x��}{R+r}$��
��$x=\frac{m{v}_{0}��R+r��}{{B}^{2}{L}^{2}}$�ã�$P��=m{v_0}-\frac{{{B^2}{L^2}x��}}{R+r}$��
ͼ����ͼ��ʾ��
��4���ɶ��ܶ�����֪��$\frac{1}{2}m{v}_{t}^{2}-\frac{1}{2}m{v}_{0}^{2}=-{F}_{��}x$��
��������ܰ��������ٶȼ�С����С�������嶯����λ�Ʊ仯��ͼ�������б�ʾ���ֵ��ʾ������������ͼ����ͼ��ʾ��
�𣺣�1����������˶����ٶ�Ϊv0ʱ��������ٶ�a�Ĵ�СΪ$\frac{{B}^{2}{L}^{2}{v}_{0}}{m��R+r��}$��
��2��������ڵ������˶���λ��xΪ$\frac{m{v}_{0}��R+r��}{{B}^{2}{L}^{2}}$��
��3���ӵ���������˶���ʼ��ʱ�����嶯����λ�Ʊ仯��ͼ����ͼ��ʾ��
��4���ӵ���������˶���ʼ��ʱ�����嶯����λ�Ʊ仯��ͼ����ͼ��ʾ��
���� ���⿼�黬�����⣬�ؼ��Ǹ��ݶ��������Ͷ��ܶ�����ʽ�õ�������������λ�Ƽ�Ĺ�ϵ��ע����ƽ���ٶȡ�ƽ��������ƽ����������ʽ������

 ��У����ϵ�д�
��У����ϵ�д�| A�� | ������ȫʧ��״̬ | B�� | ����ƽ��״̬ | ||
| C�� | ���ڳ���״̬ | D�� | ������Ҳ��ʧ�� |
 ��ͼ��ʾΪ����Ƥ������װ�ã�ת��ʱƤ���������м����������ǹ̶���һ��ģ���1�İ뾶����2�İ뾶��ͬ����3�İ뾶����4�İ뾶��ͬ����Ϊ��1����2�뾶��һ�룬����1��Ե��a�����4��Ե��c����ȣ�������
��ͼ��ʾΪ����Ƥ������װ�ã�ת��ʱƤ���������м����������ǹ̶���һ��ģ���1�İ뾶����2�İ뾶��ͬ����3�İ뾶����4�İ뾶��ͬ����Ϊ��1����2�뾶��һ�룬����1��Ե��a�����4��Ե��c����ȣ�������| A�� | ���ٶ�֮��Ϊ1��4 | B�� | ���ٶ�֮��Ϊ1��4 | ||
| C�� | ���ļ��ٶ�֮��Ϊ8��1 | D�� | ���ļ��ٶ�֮��Ϊ1��8 |
 ��ͼ��ʾ�����ʹ���ˮƽ���ֳ�ΪL���������ʺ㶨Ϊv��������˳��ٷ���ľ�飬��ľ���봫�ʹ����Ħ������Ϊ�̣���ľ�������˶����Ҷ˵�ʱ������ǣ�������
��ͼ��ʾ�����ʹ���ˮƽ���ֳ�ΪL���������ʺ㶨Ϊv��������˳��ٷ���ľ�飬��ľ���봫�ʹ����Ħ������Ϊ�̣���ľ�������˶����Ҷ˵�ʱ������ǣ�������| A�� | $\sqrt{\frac{2L}{��g}}$ | B�� | $\frac{2L}{v}$ | C�� | $\frac{L}{v}$+$\frac{v}{2��g}$ | D�� | $\frac{L}{v}$ |
 ��ͼ��ʾ���Ⱥ����ٶ�v1��v2���ٰ�һ������Ȧˮƽ�����н���ǿ�ų�������v1=2v2�������Ⱥ���������£�������
��ͼ��ʾ���Ⱥ����ٶ�v1��v2���ٰ�һ������Ȧˮƽ�����н���ǿ�ų�������v1=2v2�������Ⱥ���������£�������| A�� | ��Ȧ�еĸ�Ӧ�綯��֮��ΪE1��E2=1��2 | |
| B�� | ��Ȧ�еĸ�Ӧ����֮��ΪI1��I2=1��2 | |
| C�� | ��Ȧ�в����Ľ�����֮��Q1��Q2=1��4 | |
| D�� | ͨ����Ȧij����ĵ����֮��q1��q2=1��1 |
 ��ͼ��L������Ϊm�ĵ����ab����������ϸ��ˮƽ���ң���������ǿ�ų��У���ab��ͨ����ͼ�ĺ㶨����Iʱ��ab������ԭ��ֱ�棬��ϸ������ֱ����ɦȽǵ�λ���ٴδ��ھ�ֹ״̬����֪ab��ʼ����ų�����ֱ����Ÿ�Ӧǿ�ȵĴ�С�����ǣ�������
��ͼ��L������Ϊm�ĵ����ab����������ϸ��ˮƽ���ң���������ǿ�ų��У���ab��ͨ����ͼ�ĺ㶨����Iʱ��ab������ԭ��ֱ�棬��ϸ������ֱ����ɦȽǵ�λ���ٴδ��ھ�ֹ״̬����֪ab��ʼ����ų�����ֱ����Ÿ�Ӧǿ�ȵĴ�С�����ǣ�������| A�� | $\frac{mgtan��}{IL}$ | B�� | $\frac{mgsin��}{IL}$ | C�� | $\frac{mgsin��}{2IL}$ | D�� | $\frac{2mgsin��}{3IL}$ |
 ���̿���OOת�������̵�Բ���������ߣ�ͨ������R�����̱�Ե�ĵ�ˢb���������̰�ͼʾ����ת������ʩ��һ��ֱ����Բ�̵���ǿ�ų���������
���̿���OOת�������̵�Բ���������ߣ�ͨ������R�����̱�Ե�ĵ�ˢb���������̰�ͼʾ����ת������ʩ��һ��ֱ����Բ�̵���ǿ�ų���������| A�� | ���еĸ�Ӧ������b��O | |
| B�� | b��ĵ��Ƹ���O��ĵ��� | |
| C�� | �������涼�дų�ͨ������ͨ�����䣬����R����Ӧ���� | |
| D�� | ���Ӵų�Խǿ��Բ��Խ��ֹͣת�� |
 С��AB�����ڹ⻬��ˮƽ���ϣ�A�˹̶�һ�����ʵ��ɣ�B��ճ����Ƥ�࣬AB������ΪM����ΪL������Ϊm��ľ��C����С���ϣ���ϸ��������С����A�˲�ʹ����ѹ������ʼʱAB��C�����ھ�ֹ״̬����ͼ��ʾ����ͻȻ�ն�ϸ�������ɱ��ͷţ�ʹľ��C��B�˳�ȥ������B����Ƥ��ճ��һ������˵������ȷ���ǣ�������
С��AB�����ڹ⻬��ˮƽ���ϣ�A�˹̶�һ�����ʵ��ɣ�B��ճ����Ƥ�࣬AB������ΪM����ΪL������Ϊm��ľ��C����С���ϣ���ϸ��������С����A�˲�ʹ����ѹ������ʼʱAB��C�����ھ�ֹ״̬����ͼ��ʾ����ͻȻ�ն�ϸ�������ɱ��ͷţ�ʹľ��C��B�˳�ȥ������B����Ƥ��ճ��һ������˵������ȷ���ǣ�������| A�� | ���AB���ڱ���⻬������ϵͳ�κ�ʱ�̻�е�ܶ��غ� | |
| B�� | ����ϵͳ�κ�ʱ�̶������غ� | |
| C�� | ��ľ��Ե��˶��ٶ�Ϊvʱ��С���Ե��˶��ٶ�Ϊ$\frac{m}{M}$v | |
| D�� | ����ϵͳ���ֹ |
 ��ͼ��ʾ��������ͬ������С��A��B��C���ڹ⻬��ˮƽ���ϣ�����С��B��C��ֹ���м�����һ����ԭ�����ᵯ�ɣ�С��A���ٶ�v��С��B������ճ��һ����ײʱ�伫�̣���֮����˶��У������ɳ������ʱ��������
��ͼ��ʾ��������ͬ������С��A��B��C���ڹ⻬��ˮƽ���ϣ�����С��B��C��ֹ���м�����һ����ԭ�����ᵯ�ɣ�С��A���ٶ�v��С��B������ճ��һ����ײʱ�伫�̣���֮����˶��У������ɳ������ʱ��������| A�� | С��A��B���ٶ�Ϊ$\frac{v}{2}$��С��C���ٶ�Ϊ�� | |
| B�� | ����С����ٶȾ�Ϊ$\frac{v}{3}$ | |
| C�� | ���ɵĵ�������Ϊ$\frac{m{v}^{2}}{3}$ | |
| D�� | ���ɵĵ�������Ϊ$\frac{m{v}^{2}}{12}$ |