题目内容
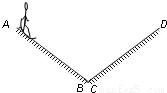
某滑雪赛道 AB、CD段可看成倾角θ=37的斜面,两斜面与装置间的动摩擦因数相同,AB、CD间有一段小圆弧相连(圆弧长度可忽略,人经圆弧轨道时机械能损失忽略不计)如图,他从静止开始匀加速下滑,经6s下滑72m到达底端,(1)求运动员刚到达AB底端时的速度大小;
(2)求装置与雪地间的动摩擦因数μ;
(3)取刚开始运动为计时起点,求第二次到达最低点经历的时间.
【答案】分析:(1)根据匀变速直线运动的位移时间公式求出加速度的大小,再根据速度时间公式求出运动员刚到达AB底端时的速度大小;
(2)根据牛顿第二定律求出动摩擦因数的大小.
(3)根据牛顿第二定律求出上滑的加速度和上滑的位移以及上滑的时间,在求出下滑的时间,从而求出第二次到达最低点经历的时间.
解答:解:(1)在AB段由x= at2
at2
v=at
代入数据得v=24m/s a=4m/s2
(2)由牛顿第二定律 a=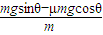
则μ=0.25
(3)运动员从C到D加速度大小a1=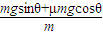 =8m/s2
=8m/s2
上升到最高点历时 t1=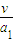 位移大小 x2=
位移大小 x2=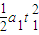
下滑过程加速度大小为a,则又滑到斜面底端历时t2=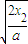
则总时间为t总=t+t1+t2=6+3+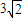 =13.2s
=13.2s
答:(1)运动员刚到达AB底端时的速度大小为24m/s.
(2)装置与雪地间的动摩擦因数为0.25.
(3)第二次到达最低点经历的时间为13.2s.
点评:加速度是联系力学和运动学的桥梁,通过加速度可以根据力求运动,也可以根据运动求力.
(2)根据牛顿第二定律求出动摩擦因数的大小.
(3)根据牛顿第二定律求出上滑的加速度和上滑的位移以及上滑的时间,在求出下滑的时间,从而求出第二次到达最低点经历的时间.
解答:解:(1)在AB段由x=
 at2
at2 v=at
代入数据得v=24m/s a=4m/s2
(2)由牛顿第二定律 a=
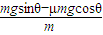
则μ=0.25
(3)运动员从C到D加速度大小a1=
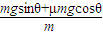 =8m/s2
=8m/s2上升到最高点历时 t1=
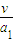 位移大小 x2=
位移大小 x2=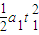
下滑过程加速度大小为a,则又滑到斜面底端历时t2=
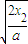
则总时间为t总=t+t1+t2=6+3+
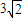 =13.2s
=13.2s答:(1)运动员刚到达AB底端时的速度大小为24m/s.
(2)装置与雪地间的动摩擦因数为0.25.
(3)第二次到达最低点经历的时间为13.2s.
点评:加速度是联系力学和运动学的桥梁,通过加速度可以根据力求运动,也可以根据运动求力.

练习册系列答案
相关题目

