题目内容
如图所示，a、b、c是在地球大气层外圆形轨道上运动的3颗人造地球卫星，下列判断正确的是（ ）| A、b卫星加速就能追上同一轨道上的c卫星 | B、b、c卫星的线速度相等且小于a卫星的线速度 | C、b卫星的角速度大于c卫星的角速度 | D、a卫星的周期大于b卫星的周期 |
分析：根据万有引力提供卫星圆周运动向心力来处理不同轨道卫星周期与角速度及线速度大小关系，根据卫星变轨原理处理卫星追及问题．
解答：解：根据万有引力提供卫星圆周运动向心力G
=m
=mr(
)2=mrω2=ma可知：
A、b卫星原本匀速圆周运动，万有引力等于圆周运动向心力，现让b卫星加速，则卫星所需向心力增加，而提供卫星圆周运动向心力的万有引力没有变化，故此时满足离心运动条件：F供＜F需，故卫星将做离心运动而抬高轨道，故b加速后不能追上同一轨道运行的c卫星，故A错误．
B、v=
，b、c卫星的半径小线速度大，故B错误（b、c线速度大小相等方向不同）；
C、角速度ω=
可知b、c半径相同，角速度大小相等，故C错误；
D、T=
可知，a卫星的半径大，故周期大，所以D正确；
故选：D
| mM |
| r2 |
| v2 |
| r |
| 2π |
| T |
A、b卫星原本匀速圆周运动，万有引力等于圆周运动向心力，现让b卫星加速，则卫星所需向心力增加，而提供卫星圆周运动向心力的万有引力没有变化，故此时满足离心运动条件：F供＜F需，故卫星将做离心运动而抬高轨道，故b加速后不能追上同一轨道运行的c卫星，故A错误．
B、v=
|
C、角速度ω=
|
D、T=
|
故选：D
点评：熟悉掌握卫星变轨原理和万有引力提供圆周运动向心力是解决此类问题的关键．
练习册系列答案
导学教程高中新课标系列答案
相关题目
如图所示，a、b、c为电场中同一电场线上的三点，且b为ac的中点，a、c电势分别为φa=8V，φc=6V．下列叙述正确的是（ ）
如图所示，A、B、C、D是某匀强电场中的4个等势面，一个质子和一个α粒子（电荷量是质子的2倍，质量是质子的4倍）同时在A等势面从静止出发，向右运动，当到达D等势面时，下列说法正确的是（ ）
如图所示，a、b和c都是厚度均匀的平玻璃板，a和b、b和c之间的夹角都为α，一细光束由红光和蓝光组成，以入射角θ从O点射入a板，且射出c板后的两束单色光通过空气射在地面上P、Q两点，由此可知（ ）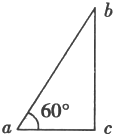
如图所示，a、b、c是匀强电场中的直角三角形的三个顶点．已知a、b、c三点的电势分别为φa=8V、φb=-4V、φc=2V，