题目内容
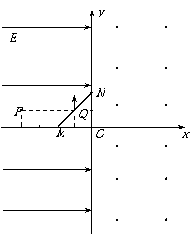
如图所示，在y轴左侧有一匀强电场，场强大小为E，方向与x轴平行且沿x轴正向，在y轴右侧有一匀强磁场，方向垂直纸面向外。现将一挡板放在第一象限内，其与x、y轴的交点M、N到坐标原点的距离均为2L。有一质量为m电荷量为+q的粒子在第二象限内从距x轴为L、y轴为4L的P点由静止释放（不计重力），粒子与挡板碰后电荷量不变，速度大小不变方向变为沿y轴正向，当粒子第一次到达y轴时电场消失。求：
（1）粒子第一次到达y轴时距坐标原点多远？
（2）若使粒子再次打到档板上，磁感应强度的大小的取值范围？
解：
（1）设粒子与板作用前瞬间，速率为
，由动能定理有
（1分）
得
（1分）
粒子与档板碰后在电场中作类平抛运动，设到达y轴时与Q点的竖距离为y，
在x轴方向有
（1分）
在y轴方向有
（1分）
由以上二式得
（1分）
（1分）
故粒子第一次到达y轴时距坐标原点为
（1分）
（2）粒子到A点时，x轴方向的速度分量为
（1分）
设
与y轴正向的夹角为
有，
，故
（1分）
此时速度
（1分）
粒子进入磁场后将做匀速率圆周运动，转过300°后打到板上的N点时，磁感强度
为最大，有
（1分）
又
（1分）
故
=
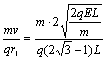（1分）
当磁感强度的大小减小到
时，粒子做半径为r2的圆周运动到达y轴上的C点，之后沿直线运动打到板上的M点。
∠OCM=30°，OC长为
（1分）
故
（1分）
同理
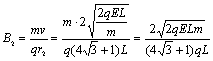（1分）
所以B的取值范围为：
≤B≤ （2分）
（2005?浦东新区一模）如图所示，在y轴左侧有一垂直于纸面向里的匀强磁场，一个圆形线圈的一半放在磁场中，圆心与原点O重合，线圈平面与磁场方向垂直．在下列做法中，能使线圈中得到顺时针方向感应电流的是（ ）
