题目内容
如图所示，宽为l的金属框架和水平面夹角为α，并处于磁感应强度为B的匀强磁场中，磁场方向垂直于框架平面．导体棒ab的质量为m，长度为d置于金属框架上时将向下匀加速滑动，导体棒与框架之间的最大静摩擦力为f．为使导体棒静止在框架上，将电动势为E，内阻不计的电源接入电路，若框架与导体棒的电阻不计，求需要接入的滑动变阻器R的阻值范围．分析：导体棒静止在框架上，导体棒受到重力、沿斜面向上的安培力，框架的支持力，当导体棒刚要上滑时，导体棒受到的静摩擦力沿斜面向下，达到最大值f，此时滑动变阻器的电阻R最小；当导体棒刚要下滑时，导体棒受到的静摩擦力沿斜面向上，达到最大值f，此时滑动变阻器的电阻R最大；由欧姆定律求出电流，安培力的大小为F=BId，根据平衡条件求出电阻的最大值和最小值，再求出阻值的范围．
解答：解：导体棒静止在斜面上，导体棒受到的安培力F=BId，I=
．
当R最小时，导体棒受到的静摩擦力沿斜面向下，达到最大值f，则有
F=mgsinα+f，又F=BId=
解得 Rmin=
当R最大时，导体棒受到的静摩擦力沿斜面向上，达到最大值f，则有
有F=mgsina-f，F=
解得 Rmax=
解得：
≤R≤
．
答：需要接入的滑动变阻器R的阻值范围是
≤R≤
．
| E |
| R |
当R最小时，导体棒受到的静摩擦力沿斜面向下，达到最大值f，则有
F=mgsinα+f，又F=BId=
| BdE |
| Rmin |
解得 Rmin=
| BEd |
| mgsinα+f |
当R最大时，导体棒受到的静摩擦力沿斜面向上，达到最大值f，则有
有F=mgsina-f，F=
| BdE |
| Rmax |
解得 Rmax=
| BEd |
| mgsinα-f |
解得：
| BEd |
| mgsinα+f |
| BEd |
| mgsinα-f |
答：需要接入的滑动变阻器R的阻值范围是
| BEd |
| mgsinα+f |
| BEd |
| mgsinα-f |
点评：本题是磁场中导体平衡问题，关键是临界条件的确定．当两物体间刚要滑动时，静摩擦力达到最大，是经常用到的临界条件．
练习册系列答案
相关题目
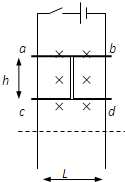（2012?嘉定区一模）如图所示，宽为L的光滑长金属导轨固定在竖直平面内，不计电阻．将两根质量均为m的水平金属杆ab、cd用长h的绝缘轻杆连接在一起，放置在轨道上并与轨道接触良好，ab电阻R，cd电阻2R．虚线上方区域内存在水平方向的匀强磁场，磁感应强度B．
键，释放两杆后能保持静止，则ab杆受的磁场力多大？
少？
度B随时间变化规律为B=kt（k为已知常数），求cd杆离开磁场前，两杆内的感应电流大小。某同学认为：上述情况中磁通量的变化规律与两金属杆静止不动时相同，可以采用Δ=ΔB·Lh 计算磁通量的改变量……该同学的想法是否正确？若正确，说明理由并求出结果；若不正确，说明理由并给出正确解答。
如图所示，宽为l的金属框架和水平面夹角为α，并处于磁感应强度为B的匀强磁场中，磁场方向垂直于框架平面．导体棒ab的质量为m，长度为d置于金属框架上时将向下匀加速滑动，导体棒与框架之间的最大静摩擦力为f．为使导体棒静止在框架上，将电动势为E，内阻不计的电源接入电路，若框架与导体棒的电阻不计，求需要接入的滑动变阻器R的阻值范围．