Question

如图所示，某生产线上相互垂直的甲乙传送带等高、宽度均为d ，均以大小为v的速度运行，图中虚线为传送带中线．一工件（视为质点）从甲左端释放，经长时间由甲右端滑上乙，滑至乙中线处时恰好相对乙静止．下列说法中正确的是（    ）

A、工件在乙传送带上的痕迹为直线，痕迹长为

B、工件从滑上乙到恰好与乙相对静止所用的时间为

C、工件与乙传送带间的动摩擦因数    

D、乙传送带对工件的摩擦力做功为零

 

Answer 1

【答案】

AD

【解析】

试题分析：物体滑上乙时，相对于乙上的那一点的速度分为水平向右的v和向后的v，合速度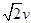，就是沿着与乙成45°的方向，那么相对于乙的运动轨迹肯定是直线，故A正确；假设它受滑动摩擦力f=μmg，方向与合相对速度在同一直线，所以角θ=45°，则相对于乙的加速度也沿这个方向，经过t后，它滑到乙中线并相对于乙静止，根据牛顿第二定律，有：μmg=ma，解得a=μg；运动距离 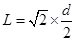．又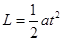，将L和a代入所以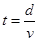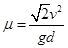，，故BC错误；滑上乙之前，工件绝对速度为v，动能为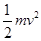；滑上乙并相对停止后，速度也是v，动能也是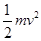；而在乙上面的滑动过程只有摩擦力做了功，动能又没变化，所以乙对工件的摩擦力做功为0，故D正确；故选AD．

考点：牛顿定律的综合应用。