题目内容
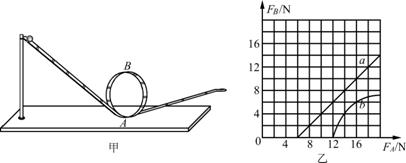
图甲为竖直放置的离心轨道，其中圆轨道的半径r=0.10m，在轨道的最低点A和最高点B各安装了一个压力传感器（图中未画出），小球（可视为质点）从斜轨道的不同高度由静止释放，可测出小球在轨道内侧通过这两点时对轨道的压力FA和FB。g取10m/s2。
（1）若不计小球所受阻力，且小球恰能过B点，求小球通过A点时速度vA的大小；
（2）若不计小球所受阻力，小球每次都能通过B点，FB随FA变化的图线如图乙中的a所示，求小球的质量m；
（3）若小球所受阻力不可忽略，FB随FA变化的图线如图乙中的b所示，求当FB=6.0N时，小球从A运动到B的过程中损失的机械能
。
（1）若小球恰能通过B点，设此时小球质量为m，通过B时的速度为vB。根据牛顿第二定律有
（2分）
根据机械能守恒定律有
（2分）
所以 
m/s
m/s（1分）
（2）根据第（1）问及图乙a图线可知：当小球通过A点时的速度m/s时，小球对B点压力为0，则小球对轨道A点压力的大小FA1=6N（1分）
设小球通过A点时，轨道对小球支持力的大小为FA2。根据牛顿运动定律有
（1分） 且 
（2分）
所以 
kg（1分）
（3）根据图乙b图线可知：当小球通过B点时，若小球对轨道压力的大小FB=6.0N，则小球通过A点时对轨道压力的大小FA=16N。设轨道对小球通过A、B时支持力的大小分别为
、
，速度分别为
、
。根据牛顿运动定律有
且 
（1分）
且 
（1分）
在小球从A运动到C的过程中，根据功能原理又有
（2分）
所以 
J（1分）
小博士期末闯关100分系列答案
名校名师培优作业本加核心试卷系列答案
。
。
。
