Question

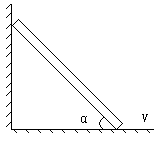
如图所示，一轻杆斜靠在竖直墙和水平地面上．当向右以速度v水平匀速拉动杆的下端点时，杆的上端点沿墙移动速度如何变化？

Answer 1

答案：
解析：

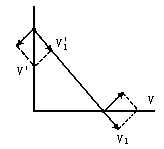
设棒与水平面成α角时，棒上端点沿墙下移速度为，v和沿杆方向速度分量相同(如图所示)． 　　　　　　　　 v1＝vcosα，  ＝cos(－α)， 因为　　　　　　　　 v1＝ ， 所以　　　　　　    ＝vcotα． 式中角α从向变化，故越来越大． 　　说明：下端点右移时杆与水平面夹角α变小，下端点右移时上端点下移．其运动方向的速度为合速度．两端点速度的关系可由杆长联系起来．

提示：

长度一定的杆两端沿杆方向的速度分量相等，这种情形还可推广到连接体问题上，即连接体在无相对运动的方向上速度(位移、加速度)分量相等．