题目内容
如图所示，两木块质量分别是m1、m2，用劲度系数为k的轻弹簧连在一起，放在水平面上，将木块1下压一段距离后释放，它将做简谐运动．在运动过程中，木块2始终没有离开水平面．且对水平面的最小压力为零，则木块1的最大加速度大小是多少？木块2对水平面的最大压力为多少？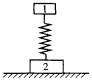
答案：见详解
解析：
提示：
解析：
| 木块1的最大加速度为
a= 其方向竖直向下． 当弹簧处于压缩状态且压缩量最大时，木块2对水平面压力最大，设为Nmax．与此同时，木块1到达最低点，根据简谐运动的对称性．木块1此时的加速度大小也为a，方向竖直向上，说明超重部分为m1a．对两木块、弹簧组成的系统有：Nmax等于两木块的重力与木块1的超重部分之和，即 Nmax=(m1+m2)g+m1a ② 由①、②式联立解得 Nmax=2(m1+m2)g |
①提示：
| 由题意可知，当弹簧的伸长量最大时，木块1到达最高点，其所受的合力最大，加速度也最大．与此同时，弹簧对木块2的拉力也最大，木块2对水平面的压力为零．这表明此时两木块、弹簧组成的系统处于完全失重状态，即木块1的失重部分等于两木块的重力之和，即m1a=(m1+m2)g． |
练习册系列答案
相关题目
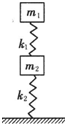如图所示，两木块质量分别为m1和m2，两轻质弹簧的劲度系数分别为k1，和k2，上面木块压在弹簧上（但不拴接），整个系统处于静止状态．现缓慢向上提m1木块，直到m1木块刚离开上面弹簧，在这过程中下面木块移动的距离为
A.
[来源:Z|xx|k.Com]