题目内容
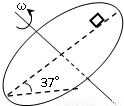如图所示，倾斜放置的圆盘绕着中轴匀速转动，圆盘的倾角为37°，在距转动中心r=0.1m处放一个小木块，小木块跟随圆盘一起转动，小木块与圆盘间的动摩擦因数为μ=0.8，假设木块与圆盘的最大静摩擦力与相同条件下的滑动摩擦力相同．若要保持小木块不相对圆盘滑动，圆盘转动的角速度最大不能超过（ ）A．2 rad/s
B．8 rad/s
C．
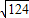rad/sD．
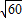rad/s
【答案】分析：因为木块在最低点时所受的静摩擦力方向沿圆盘向上，最高点的所受的静摩擦力等于最低点的静摩擦力，可知只要小木块转过最低点时不发生相对滑动就能始终不发生相对滑动．根据牛顿第二定律求出圆盘转动的最大角速度．
解答：解：只要小木块转过最低点时不发生相对滑动就能始终不发生相对滑动，设其经过最低点时所受静摩擦力为f，由牛顿第二定律有f-mgsinθ=mrω2；为保证不发生相对滑动需要满足f≤μmgcosθ．联立解得ω≤2rad/s．故A正确，B、C、D错误．
故选A．
点评：解决本题的关键知道只要小木块转过最低点时不发生相对滑动就能始终不发生相对滑动，结合牛顿第二定律和最大静摩擦力进行求解．
解答：解：只要小木块转过最低点时不发生相对滑动就能始终不发生相对滑动，设其经过最低点时所受静摩擦力为f，由牛顿第二定律有f-mgsinθ=mrω2；为保证不发生相对滑动需要满足f≤μmgcosθ．联立解得ω≤2rad/s．故A正确，B、C、D错误．
故选A．
点评：解决本题的关键知道只要小木块转过最低点时不发生相对滑动就能始终不发生相对滑动，结合牛顿第二定律和最大静摩擦力进行求解．
练习册系列答案
相关题目
如图所示，倾斜放置的圆盘绕着中轴匀速转动，圆盘的倾角为37°，在距转动中心r=0.1m处放一个小木块，小木块跟随圆盘一起转动，小木块与圆盘间的动摩擦因数为μ=0.8，假设木块与圆盘的最大静摩擦力与相同条件下的滑动摩擦力相同．若要保持小木块不相对圆盘滑动，圆盘转动的角速度最大不能超过（ ）
如图所示，倾斜放置的传送带顺时针方向转动，现将木块A无初速地放在传送带上，下列分析正确的是（ ）
如图所示，倾斜放置的无限长金属导轨上端接在定值电阻R，其余电阴忽略不计，质量为m的金属棒AB由静止开始释放，在其下滑过程中，下列说法中正确的是（ ）
如图所示，倾斜放置的圆盘绕着中轴匀速转动，圆盘的倾角为37°，在距转动中心0.1m处放一小木块，小木块跟随圆盘一起转动，小木块与圆盘的动摩擦因数为0.8，木块与圆盘的最大静摩擦力与相同条件下的滑动摩擦力相同．若要保持小木块不相对圆盘滑动，圆盘转动的角速度最大值为（ ）（sin37°=0.6，cos37°=0.8）
rad/s D.
rad/s