题目内容
如图(a)所示,木板与水平面间的夹角θ可以随意改变,可视为质点的小物块从木板的底端以大小恒定的初速率v0沿木板向上运动,所能上升的最大距离记为s,今改变θ而使s随之改变,根据所测量的若干组数据可以描绘出“s-θ”曲线如图(b)所示,若木板足够长,重力加速度g取10m/s2,试根据“s-θ”曲线和相关的物理规律,
求:(1)小物块的初速率v0;
(2)小物块与木板间的动摩擦因数μ;
(3)对应于“s-θ”曲线上s取最小值的P点的坐标值(θ0,smin)
 |
【答案】
(1)由图像可知 当θ1=π/2时,s1=5m,此时小物块做竖直上抛运动
可得: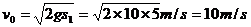
(2)由图像可知 当θ2=0时,s2=10m,此时木板水平
由牛顿第二定律得:-μmg=ma
又匀变速位移与速度关系得: 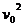 =2a
s2
=2a
s2
所以 μ=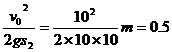
(3)当板与水平方向夹角为θ时,沿斜面上滑的距离为s,
由动能定理得:0-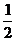 m
m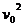 =-mgssinθ-μmgscosθ
=-mgssinθ-μmgscosθ
即 S=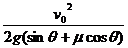
令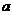 =sinθ+μcosθ=
=sinθ+μcosθ=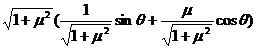
设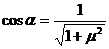 所以
所以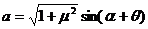 ,
,
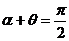 时,
时,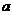 存在最大值
存在最大值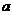 m=
m=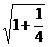 =
=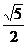 ,
,
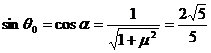

对应s的最小值为smin=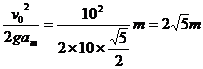
P点的坐标值( ,
,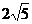 )
)

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
如图(a)所示,木板OA可绕轴O在竖直平面内转动,某研究小组利用此装置探索物块在方向始终平行于木板向上、大小为F=8N的力作用下加速度与倾角的关系.已知物块的质量m=1kg,通过DIS实验,描绘出了如图(b)所示的加速度大小a与倾角θ的关系图线(θ<90°).若物块与木板间的动摩擦因数为0.2,假定物块与木板间的最大静摩擦力始终等于滑动摩擦力,g取10m/s2.则下列说法中正确的是( )

| A、由图象可知木板与水平面的夹角处于θ1和θ2之间时,物块所受摩擦力一定为零 | ||
| B、由图象可知木板与水平面的夹角大于θ2时,物块所受摩擦力一定沿木板向上 | ||
| C、根据题意可以计算得出物块加速度a0的大小为6 m/s2 | ||
D、根据题意可以计算当θ=45°时,物块所受摩擦力为f=μmgcos45°=
|
 (2011?陕西二模)如图(a)所示,木板与水平面间的夹角θ可以在0到π/2内随意改变,可视为质点的小物块从木板的底端以大小恒定的初速率v0沿木板向上运动,所能上升的最大距离记为x,今改变θ而使x随之改变,根据所测量的若干组数据可以描绘出x-θ曲线如图(b)所示,若木板足够长,重力加速度g取10m/s2,试根据x-θ曲线和相关的物理规律,求:
(2011?陕西二模)如图(a)所示,木板与水平面间的夹角θ可以在0到π/2内随意改变,可视为质点的小物块从木板的底端以大小恒定的初速率v0沿木板向上运动,所能上升的最大距离记为x,今改变θ而使x随之改变,根据所测量的若干组数据可以描绘出x-θ曲线如图(b)所示,若木板足够长,重力加速度g取10m/s2,试根据x-θ曲线和相关的物理规律,求:



