��Ŀ����
��ͼ��ʾ������A��B���ᵯ�������ӣ����ڹ⻬��ˮƽ���ϣ�����A��������������B������������B�������ֱǽ����Ӵ������ɱ�ѹ�������е�������ΪE���ͷź�����A�����˶�������������B�뿪���ǽ�ڣ�����B�뿪ǽ�ں���A��B�͵�����ɵ�ϵͳ���������˶��Ĺ����У�����˵�����ٵ����쳤���ʱ�ĵ������ܵ��ڵ���ѹ�����ʱ�ĵ������ܣ��ڵ����쳤���ʱ�ĵ�������С�ڵ���ѹ�����ʱ�ĵ������ܣ�������B������ܵ���E��������B�������С��E��������ȷ���ǣ�������

| A���٢� | B���٢� | C���ڢ� | D���ڢ� |

��������B�뿪ǽ�ڵ�˲��A���ٶ�Ϊv�������ϵͳ�Ļ�е���غ�ã�
E=
mAv2
����B�뿪ǽ�ں�ϵͳ�Ķ����غ㣬�������쳤���ʱ��ѹ�����ʱ����������ٶ���ȣ���
mAv=��mA+mB��v�䣬��֪����״̬�£�A��B��ͬ�ٶ���ͬ��������ͬ������ݻ�е���غ�֪�������쳤���ʱ�ĵ������ܵ��ڵ���ѹ�����ʱ�ĵ������ܣ��ʢ���ȷ���ڴ���
�ۡ��ܵ��ɴ�B�뿪ǽ�ڵ���һ�λָ�ԭ���Ĺ��̣�Bһֱ���٣����ɵ�һ�λָ�ԭ��ʱB���ٶ����
���ʱA��B���ٶȷֱ�ΪvA��vB��
���ݶ����غ�ͻ�е���غ�ã�
mAv=mAvA+mBvB
mAv2=
mA
+
mB
��ã�vB=
v
����B�������ΪEkB=
mB
=
mB(
)2v2=
mAv2?
=
E
����֪��mA��mB��EkB��E���ʢ۴�����ȷ��
��ѡB
E=
| 1 |
| 2 |
����B�뿪ǽ�ں�ϵͳ�Ķ����غ㣬�������쳤���ʱ��ѹ�����ʱ����������ٶ���ȣ���
mAv=��mA+mB��v�䣬��֪����״̬�£�A��B��ͬ�ٶ���ͬ��������ͬ������ݻ�е���غ�֪�������쳤���ʱ�ĵ������ܵ��ڵ���ѹ�����ʱ�ĵ������ܣ��ʢ���ȷ���ڴ���
�ۡ��ܵ��ɴ�B�뿪ǽ�ڵ���һ�λָ�ԭ���Ĺ��̣�Bһֱ���٣����ɵ�һ�λָ�ԭ��ʱB���ٶ����
���ʱA��B���ٶȷֱ�ΪvA��vB��
���ݶ����غ�ͻ�е���غ�ã�
mAv=mAvA+mBvB
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2A |
| 1 |
| 2 |
| v | 2B |
��ã�vB=
| 2mA |
| mA+mB |
����B�������ΪEkB=
| 1 |
| 2 |
| v | 2B |
| 1 |
| 2 |
| 2mA |
| mA+mB |
| 1 |
| 2 |
| 4mAmB |
| (mA+mB)2 |
| 4mAmB |
| (mA+mB)2 |
����֪��mA��mB��EkB��E���ʢ۴�����ȷ��
��ѡB

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
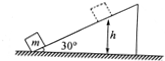


 ���������˶������A����Ħ�����ơ��������˶�ʱ����ɰ��H�ߴ���һ����Ϊm��m=M���������������䣬ǡ������ɰ���С������Ժ���˶������У������Ե����ܵ����ֵ��
���������˶������A����Ħ�����ơ��������˶�ʱ����ɰ��H�ߴ���һ����Ϊm��m=M���������������䣬ǡ������ɰ���С������Ժ���˶������У������Ե����ܵ����ֵ��