Question

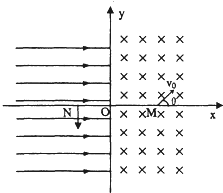（2011?周口模拟）在xOy平面内，x＞0的区域存在垂直纸面向里的匀强磁场，磁感应强度为B=0.4T；x＜0的区域存在沿x轴正方向的匀强电场．现有一质量为m=4.0×10^-9 kg，带电荷量为q=2.0×10^-7 C的正粒子从x轴正方向上的M点以速度v₀=20m/s进入磁场，如图所示，v₀与x轴正方向的夹角θ=45°，M点与O点相距为l=

2

m．已知粒子能以沿着y轴负方向的速度垂直穿过x轴负半轴上的N点，不计粒子重力．求：（1）粒子穿过y轴正半轴的位置以及此时速度与y轴负方向的夹角；
（2）x＜0区域电场的场强；
（3）试问粒子能否经过坐标原点O？若不能，请说明原因；若能，请求出粒子从M点运动到O点所经历的时间．

Answer 1

分析：粒子在磁场中由洛伦兹力提供向心力，做匀速圆周运动，则可求出轨道半径．由几何关系可求出PM及OP长度，再由圆的对称性可确定速度与y轴的夹角．
将曲线运动分解成x轴与y轴方向，然后由运动学公式可求出运动时间，进而可得出电场强度．
由运动轨迹及周期公式来确定粒子在磁场中运动的时间．

解答：解：（1）粒子在磁场中做匀速圆周运动时，由洛伦兹力提供向心力
   Bqv0=m

v 2 0

R

  
 得：R=1 m     
过M点做初速度v₀的垂线交y轴正方向于P点，则
PM=

l

cos45°

得：PM=2 m=2R     
由几何关系得PM为轨迹圆的直径，P点即为粒子穿过y轴正半轴的位置
OP=PMsin45°=

2

m   
由圆的对称性得粒子经过此处时的速度与y轴负方向的夹角为θ=45°．
（2）设粒子由P点到N点历时t₁，则：
x轴方向：v₀sin45°-

Eqt1

m

=0  
y轴方向：v₀t₁cos45°=OP  
联立求解，代入数据得：t₁=0.1 s，
E=2

2

v/m  （2分）
（3）粒子能到达O点
粒子在磁场中的运动周期为：T=

2πm

Bq

从M点运动到O点经过的轨迹如图
经历的时间为：t=

T

2

+

3

4

T+2t₁
代入数据得：t=（

π

8

+0.2）s≈0.59 s

点评：曲线运动可分解成两个简单的直线运动，从而由运动学与力学知识来求解．当粒子做圆周运动时，则通过定圆心、画轨迹、求半径来求解．