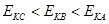题目内容
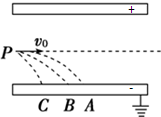分别将带等量正电的三个等质量小球，以不同的水平速度由P点射入水平放置的平行金属板间，已知上板带正电，下板接地．三小球分别落在图中A、B、C三点，则（ ）| A、三小球在电场的加速度大小相等； | B、三小球在电场中加速度大小关系是aA＜aB＜aC | C、三小球在电场中运动时间tA=tB=tC | D、三小球到达下板时的动能关系是EKC＜EKB＜EKA |
分析：小球在电场中做类平抛运动，根据运动的合成与分解，运用牛顿第二定律和运动学公式处理类平抛问题即可．
解答：解：带电小球沿垂直电场方向进入电场后均做类平抛运动，水平方向做匀速直线运动，竖直方向做匀加速直线运动．则有题意有：
A、B、三个小球所受的重力和电场力都相同，合外力相同，根据牛顿第二定律得知，三个小球的加速度相同．故A正确，B错误．
C、三个小球在竖直方向位移有：yA=yB=yC，它们的加速度相同，而小球在竖直方向做初速度为0的匀加速直线运动，由y=
at2得知它们的时间相等，即tA=tB=tC．故C正确．
D、三个小球在水平方向位移有：xA＞xB＞xC，因为在水平方向做匀速直线运动，故满足x=v0t，则得初速度v0=
，可知，初速度大小关系为：vA＞vB＞vC．
由于合外力相同，合外力对三个小球所做的功相等，根据动能定理得知，动能的增加量相等．由于vA＞vB＞vC，所以有三个微粒到达下板时的动能关系是EkA＞EkB＞EkC ．故D正确．
故选：ACD．
A、B、三个小球所受的重力和电场力都相同，合外力相同，根据牛顿第二定律得知，三个小球的加速度相同．故A正确，B错误．
C、三个小球在竖直方向位移有：yA=yB=yC，它们的加速度相同，而小球在竖直方向做初速度为0的匀加速直线运动，由y=
| 1 |
| 2 |
D、三个小球在水平方向位移有：xA＞xB＞xC，因为在水平方向做匀速直线运动，故满足x=v0t，则得初速度v0=
| x |
| t |
由于合外力相同，合外力对三个小球所做的功相等，根据动能定理得知，动能的增加量相等．由于vA＞vB＞vC，所以有三个微粒到达下板时的动能关系是EkA＞EkB＞EkC ．故D正确．
故选：ACD．
点评：处理类平抛问题的关键是利用运动的分解法，将曲线运动分解成两个方向上的直线运动，利用等时性，根据牛顿第二定律和运动学公式结合进行处理即可．
练习册系列答案
相关题目
真空中固定两个等量（电量为Q）异种点电荷A、B，A带负电，B带正电，距离为d，它们产生的电场在很远处的电势为零．竖直虚线为AB的垂直平分线．两个带等量（电量为q）异种电荷的小球用一根绝缘刚性轻杆相连，杆长为L，且L＜d，现将两个小球从很远处移到图中I所示位置（过程1），接着使用细杆绕其中心逆时针转过90°（过程2），再平移到图中II所示位置（过程3）．以W1、W2、W3分别表示上述三个过程中电场力对两个小球做功和，则（ ）
；
；
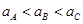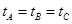