题目内容
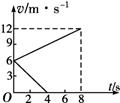
两个完全相同的物块A、B，质量均为m＝0．8 kg，在同一粗糙水平面上以相同的初速度从同一位置开始运动。图中的两条直线分别表示A物块受到水平拉力F作用和B物块不受拉力作用的v－t图象，求：
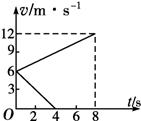
（1）物块A所受拉力F的大小；
（2）8 s末物块A、B之间的距离x。
【答案】
60 m
【解析】设A、B两物块的加速度分别为a1、a2，由v－t图象可知：A、B的初速度v0=6m/s，A物体的末速度v1=12m/s ，B物体的末速度v2=0，
a1＝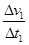
＝
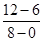m/s2＝0．75 m/s2 ①（1分）a2＝
＝
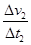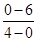m/s2＝－1．5 m/s2 ② （1分）
负号表示加速度方向与初速度方向相反。
对A、B两物块分别由牛顿第二定律得：
F－Ff＝ma1③ （1分） －Ff＝ma2④ （1分）
由①～④式可得：F＝1．8 N （1分）
（2） 设A、B两物块8 s内的位移分别为x1、x2由图象得：
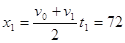m （2分）
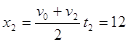m（2分）
所以x＝x1－x2＝60 m （1分）
本题考查牛顿第二定律的应用和对速度时间图像的考查，根据速度时间图像的斜率表示加速度大小，求得两个过程中加速度大小，施加拉力时有F－Ff＝ma1，撤去拉力后只受摩擦力作用，再由牛顿第二定律进行运算可求得拉力和摩擦力的值，在匀变速直线运动中平均速度等于初速度与末速度和的一半，求得平均速度再求位移大小
练习册系列答案
相关题目
（2012?葫芦岛模拟）两个完全相同的物块A、B，质量均为m=0.8kg，在同一粗糙水平面上以相同的初速度从同一位置开始运动．图中的两条直线分别表示A物块受到水平拉力F作用和B物块不受拉力作用的v-t图象，求：
两个完全相同的物块a、b，在水平面上以相同的初速度从同一位置开始运动，图中a直线表示a物体不受拉力作用、b直线表示b物体受到水平拉力F=1.8N作用的υ-t图象，求：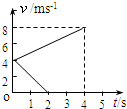
两个完全相同的物块A、B，质量均为m=0.8kg，沿同一粗糙水平面以相同的初速度从同一位置运动，它们速度随时间的变化关系如图所示，图中的两条直线分别表示A物块受到水平拉力F作用和B物块不受拉力作用的v-t图象．求：
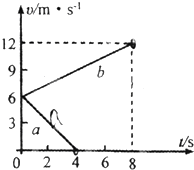两个完全相同的物块a、b质量为m=0.8kg，在水平面上以相同的初速度从同一位置开始运动，图中的两条直线表示物体受到水平拉力F作用和不受拉力作用的υ-t图象，求：
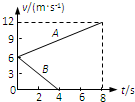两个完全相同的物块A、B质量均为m=0.8kg，在同一粗糙水平面上以相同的初速度从同一位置开始运动．图中的两条直线分别表示受到水平拉力F作用的A物块和不受拉力作用的B物块的v-t图线．取g=10m/s2．求：