题目内容
（2011?泰兴市模拟）如图所示，物体A的质量m=3kg，用两根轻绳B、C连接于竖直墙上，要使两绳都能绷直，即物体A在如图所示位置保持平衡，现施加一个力F作用于物体，力F的方向如图所示，若夹角θ=60°，求力F的大小应满足的条件．（取g=10m/s2）分析：对小球受力分析，然后根据平衡条件并运用正交分解法，得到F与两个绳子拉力的关系式再求解范围．
解答：解：A球受力如图所示，则有
水平方向：Fcosθ=FBcosθ+FC ①
竖直方向：Fsinθ+FBsinθ=mg ②
由②式得
F=
-FB≤
=20
N=34.6N
由①、②式得
F=
+
≥10
N=17.3N
所以力F大小应满足的条件是17.3 N≤F≤34.6 N．
水平方向：Fcosθ=FBcosθ+FC ①
竖直方向：Fsinθ+FBsinθ=mg ②
由②式得
F=
| mg |
| sinθ |
| mg |
| sinθ |
| 3 |
由①、②式得
F=
| mg |
| 2sinθ |
| FC |
| 2cosθ |
| 3 |
所以力F大小应满足的条件是17.3 N≤F≤34.6 N．
点评：本题是物体平衡中极值问题，也可以直接寻找临界条件：当力F最小时，OC绳松驰，张力为零；当力F最大时，OB绳松驰，张力为零；根据平衡条件分别求出力F的最小值和最大值，再求出力F的范围．
练习册系列答案
相关题目
（2011?泰兴市模拟）如图斜面ABC，AB段是光滑的，BC段是有摩擦．某物体从A点由静止开始下滑，当滑至C点时恰好停止，则下列说法正确的是（ ）
（2011?泰兴市模拟）在如图所示装置中，两物体质量分别为m1、m2，悬点a、b间的距离远大于滑轮的直径，不计一切摩擦，整个装置处于静止状态．由图可知（ ）
（2011?泰兴市模拟）物体m静止与斜面体M一起静止在水平面上．若将斜面的倾角A稍微增大一些，且物体m仍然静止在斜面上，则（ ）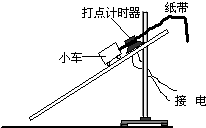
（2011?泰兴市模拟）某同学用图所示的实验装置研究小车在斜面上的运动．实验步骤如下：
