题目内容
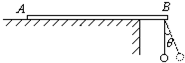
一根长为1m、质量为0.2kg的均匀直尺AB放在水平桌面上，有20cm长的一段伸在桌面之外，今在它的一端用细线悬挂一个质量为0.1kg的小球．现将小球拉起，使悬线与竖直方向成θ角，如图所示，然后由静止释放小球，若小球摆到最低位置时，直尺仅对桌面边缘有压力，则θ的角度数为90°
90°
．分析：根据力矩平衡求出绳子的拉力，再根据牛顿第二定律求出小球在最低点的速度，最后根据机械能守恒定律求出θ的角度．
解答：解：根据力矩平衡有：
mg×
l=
mg×
l+F×
l
解得F=3N．
在最低点，根据牛顿第二定律得，F-mg=m
小球摆到最低点的过程中机械能守恒，有mgr（1-cosθ）=
mv2
联立两式解得：θ=90°
故答案为：90°．
| 4 |
| 5 |
| 2 |
| 5 |
| 1 |
| 5 |
| 1 |
| 10 |
| 1 |
| 5 |
解得F=3N．
在最低点，根据牛顿第二定律得，F-mg=m
| v2 |
| r |
小球摆到最低点的过程中机械能守恒，有mgr（1-cosθ）=
| 1 |
| 2 |
联立两式解得：θ=90°
故答案为：90°．
点评：解决本题的关键掌握力矩平衡，以及能够熟练运用牛顿第二定律和机械能守恒定律．
练习册系列答案
相关题目
如图所示，一根长为1m的轻杆OA，O端用铰链固定，另一端固定着一个质量为1kg的小球A，轻杆靠在一个质量为2kg、高为0.3m物块上．若物块与地面摩擦不计，则当物块向右运动至杆与水平方向夹角为370时，轻杆的角速度为3rad/s，此时物块的动能为
