题目内容
有一玩具汽车绝缘上表面固定一个带负电物块,它们的总质量m=0.5kg,物块带电量q=-5.0×10-5c.现把玩具汽车放置在如图所示的水平直轨道A点,BC由光滑管道弯曲而成的半圆轨道,玩具汽车在光滑管道中能自由运动,整个轨道所处空间存在竖直向下的匀强电场,其电场强度大小E=6.0×l04N/c.玩具汽车在水平直轨道运动时阻力恒为Ff=0.5N,通电后玩具汽车以恒定功率P=l0w行驶,通电1.0s自动断电,断电后玩具汽车能以一定的速度从B点进入半圆轨道.已知AB间距L=4.0m,g取l0m/s2(玩具汽车可看成质点,整个运动过程物块带电量不变).①若半圆轨道半径R=0.4m,玩具汽车进入管道中B点时对管道的压力多大?
②当半圆轨道半径R满足什么条件时,玩具汽车能再次回到A点?

【答案】分析:(1)对从A到B过程运用动能定理得到B点速度,然后根据向心力公式和牛顿第二定律列式求解物体B点的压力;
(2)玩具车可能从最高点做平抛运动飞到A点,也有可能沿原路返回到A点,因此要分两种情况讨论;对于第一种情况,相距类平抛运动的位移公式求出初速度,再对从A到C过程运用动能定理求出圆轨道半径;对于第二种情况,先求出恰好不能飞离圆轨道的最高点速度,再对从A到C过程运用动能定理求出圆轨道半径.
解答:解:(1)对AB段:Pt-FfL= mv12-0
mv12-0
对B点:FN-(mg-qE)=m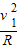
FN=42N
故玩具汽车进入管道中B点时,对管道的压力也为42N,方向竖直向下.
(2)对BC段: mv12=2R ( mg-qE)+
mv12=2R ( mg-qE)+ mv22
mv22
对类平抛:mg-qE=ma
2R= at12
at12
L=v2t1
由上二式得到:当R=1m时恰能回到A点.
另一方面,若不能从最高点射出,则
由 mv12=2R(mg-qE)+
mv12=2R(mg-qE)+ mv22 和 v2=0 得:
mv22 和 v2=0 得:
R=2m
当轨道半径R>2m时,玩具汽车将沿半圆轨道返回,由B向A运动,
根据:-Ffx=0- mv12
mv12
X=16m>4m,能回到A点.
故当半径等于1m或者大于2m时,物体能回到A点.
点评:本题第二问关键是要分两种情况讨论,对于两种情况,都是先求出C点速度,然后对A到C过程运用动能定理列式求解出轨道半径.
(2)玩具车可能从最高点做平抛运动飞到A点,也有可能沿原路返回到A点,因此要分两种情况讨论;对于第一种情况,相距类平抛运动的位移公式求出初速度,再对从A到C过程运用动能定理求出圆轨道半径;对于第二种情况,先求出恰好不能飞离圆轨道的最高点速度,再对从A到C过程运用动能定理求出圆轨道半径.
解答:解:(1)对AB段:Pt-FfL=
 mv12-0
mv12-0 对B点:FN-(mg-qE)=m
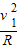
FN=42N
故玩具汽车进入管道中B点时,对管道的压力也为42N,方向竖直向下.
(2)对BC段:
 mv12=2R ( mg-qE)+
mv12=2R ( mg-qE)+ mv22
mv22 对类平抛:mg-qE=ma
2R=
 at12
at12 L=v2t1
由上二式得到:当R=1m时恰能回到A点.
另一方面,若不能从最高点射出,则
由
 mv12=2R(mg-qE)+
mv12=2R(mg-qE)+ mv22 和 v2=0 得:
mv22 和 v2=0 得:R=2m
当轨道半径R>2m时,玩具汽车将沿半圆轨道返回,由B向A运动,
根据:-Ffx=0-
 mv12
mv12 X=16m>4m,能回到A点.
故当半径等于1m或者大于2m时,物体能回到A点.
点评:本题第二问关键是要分两种情况讨论,对于两种情况,都是先求出C点速度,然后对A到C过程运用动能定理列式求解出轨道半径.

练习册系列答案
相关题目



