题目内容
如图所示，AB是匀强电场中的一条水平线段，长度为L，它与电场方向成θ角，某时刻一质量为m，带电量为+q的小球在电场中的A点由静止释放，小球沿直线AB运动到B点时离开电场，然后落到倾角为α的绝缘弹性斜面上的C点，C点距离AB高度为h，小球恰好能够沿原路返回A点，求：（1）电场强度E的大小；
（2）角α的值；
（3）球从A点出发返回A点的时间．
分析：（1）由于带电粒子做的直线运动，对带电粒子受力分析可知，粒子在电场中的受到的合力沿水平方向，在竖直方向上受力平衡，由此可以求得电场强度的大小；
（2）粒子离开电场后做的是平抛运动，水平方向的速度即为在电场中加速获得的速度的大小，竖直速度为做自由落体的末速度，由水平和竖直速度可得斜面倾角
（3）由AB的匀加速运动可得时间，然后再由平抛的自由落体得到下来时间，时间之和的两倍就是往返时间．
（2）粒子离开电场后做的是平抛运动，水平方向的速度即为在电场中加速获得的速度的大小，竖直速度为做自由落体的末速度，由水平和竖直速度可得斜面倾角
（3）由AB的匀加速运动可得时间，然后再由平抛的自由落体得到下来时间，时间之和的两倍就是往返时间．
解答：（1）由于出电场后球做平抛运动，在电场内运动时，受力如图：
其速度方向是水平的，
即合外力是水平的，由qEsinθ=mg得：
E=
（2）在电场中运动的加速度：
a=
=gcotθ；
故出电场的速度：
v0=
=
出电场后只受重力作用获得速度：v′=
斜面应与v0与v′的合速度v垂直，所以：
tanα=
=
（3）求在电场中匀速运动，故球出电场的时间：t1=
=
出电场后球做自由落体，落地时间为：t2=
t2=
=
所以往返时间：T=2（t1+t2）=2(
+
)
答：
（1）电场强度E的大小为E=
；
（2）角α的值为tanα=
；
（3）球从A点出发返回A点的时间为2(
+
)．
其速度方向是水平的，即合外力是水平的，由qEsinθ=mg得：
E=
| mg |
| qsinθ |
（2）在电场中运动的加速度：
a=
| mgcotθ |
| m |
故出电场的速度：
v0=
| 2aL |
| 2gLcotθ |
出电场后只受重力作用获得速度：v′=
| 2gh |
斜面应与v0与v′的合速度v垂直，所以：
tanα=
| v0 |
| v′ |
|
（3）求在电场中匀速运动，故球出电场的时间：t1=
| 2L |
| v0 |
|
出电场后球做自由落体，落地时间为：t2=
| ||
| g |
| ||
| g |
|
所以往返时间：T=2（t1+t2）=2(
|
|
答：
（1）电场强度E的大小为E=
| mg |
| qsinθ |
（2）角α的值为tanα=
|
（3）球从A点出发返回A点的时间为2(
|
|
点评：在题目中告诉粒子在电场中做直线运动，由此可以得出，粒子在电场中做的应该是匀加速直线运动，这是本题中的关键所在．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
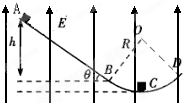如图所示，AB是一倾角为θ=37°的绝缘粗糙直轨道，滑块与斜面间的动摩擦因数μ=0.30，BCD是半径为R=0.2m的光滑圆弧轨道，它们相切于B点，C为圆弧轨道的最低点，整个空间存在着竖直向上的匀强电场，场强E=4.0×103N/C，质量m=0.20kg的带电滑块从斜面顶端由静止开始滑下．已知斜面AB对应的高度h=0.24m，滑块带电荷q=-5.0×10-4C，取重力加速度g=10m/s2，sin37°=0.60，cos37°=0.80．求：
如图所示，ab是半径为1m的金属圆环的
如图所示，在一匀强磁场中有一U形导体框bacd，线框处于水平面内，磁场与线框平面垂直，R为一电阻，ef为垂直于ab的一根导体杆，它可以在ab、cd上无摩擦地滑动，杆ef及线框中导体的电阻都可不计．开始时，给ef一个向右的初速度，则（ ）| A、ef将减速向右运动，但不是匀减速 | B、ef将匀速向右运动，最后停止 | C、ef将匀速向右运动 | D、ef将做往复运动 |
