题目内容
质量m=2×103kg,汽车以10m/s的速度通过某凸形桥的最高点时,受到桥面的支持力N=1.5×104N,取g=10m/s2,则桥面的半径为多少?当车速v为多大时,车在桥最高点时对桥面的压力恰好为零?
【答案】分析:汽车通过某凸形桥的最高点时由重力和桥面支持力的合力提供向心力,根据牛顿第二定律求解桥面的半径.当车在桥最高点时对桥面的压力恰好为零时,由重力提供汽车的向心力,再由牛顿第二定律求解v.
解答:解:桥面的半径为r,由向心力公式可知
mg-N=M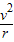
代入数据解得 r=40m
当车在桥最高点时对桥面的压力恰好为零时,设此时汽车速度为v,有mg=m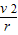
代入数据解得 v=20 m/s
答:桥面的半径为40m;当车速v为20m/s时,车在桥最高点时对桥面的压力恰好为零.
点评:本题生活中圆周运动问题,关键是分析物体的受力情况,确定向心力的来源.
解答:解:桥面的半径为r,由向心力公式可知
mg-N=M
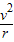
代入数据解得 r=40m
当车在桥最高点时对桥面的压力恰好为零时,设此时汽车速度为v,有mg=m
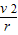
代入数据解得 v=20 m/s
答:桥面的半径为40m;当车速v为20m/s时,车在桥最高点时对桥面的压力恰好为零.
点评:本题生活中圆周运动问题,关键是分析物体的受力情况,确定向心力的来源.

练习册系列答案
相关题目