题目内容
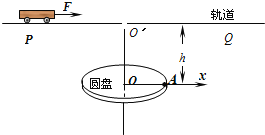
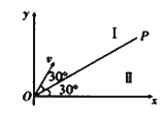
【题目】如图所示，在空间有一坐标系xOy中，直线OP与x轴正方向的夹角为30o，第一象限内有两个方向都垂直纸面向外的匀强磁场区域I和II，直线OP是它们的边界，OP上方区域I中磁场的磁感应强度为B。一质量为m，电荷量为q的质子（不计重力）以速度v从O点沿与OP成30o角的方向垂直磁场进入区域I，质子先后通过磁场区域I和II后，恰好垂直打在x轴上的Q点（图中未画出），则下列说法正确的是
A. 区域II中磁感应强度为
B. 区域II中磁感应强度为3B
C. 质子在第一象限内的运动时间为
D. 质子在第一象限内的运动时间为
【答案】D
【解析】
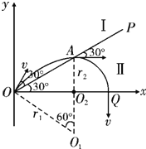
AB、设质子在磁场I和II中做圆周运动的轨道半径分别为
和
,区域II中磁感应强度为B',运动轨迹如图所示：
由牛顿第二定律得:
①
②
由带电粒子才磁场中运动的对称性和几何关系可以知道,质子从A点出磁场I时的速度方向与OP的夹角为
,故质子在磁场I中轨迹的圆心角为
,如图所示:
由几何关系可知
③,
在区域II中,质子运动1/4圆周,
是粒子在区域II中做圆周运动的圆心,
④
由①②③④计算得出区域II中磁感应强度为:
,故AB错误；
CD、质子在Ⅰ区运动轨迹对应的圆心角为,
在Ⅱ区运动轨迹对应的圆心角为
:,
质子在Ⅰ区的运动时间
,
质子在Ⅱ区运动时间
,则粒子在第一象限内的运动时间为
.故C错误,D正确.
故选D
练习册系列答案
阅读快车系列答案
相关题目
