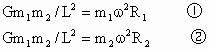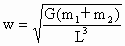题目内容
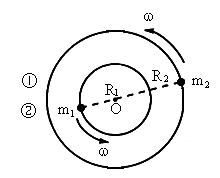
宇宙中两颗相距较近的天体称为“双星”,它们以二者连线上的某一点为圆心做匀速圆周运动,而不致因万有引力的作用吸引到一起.(1)试证:它们的轨道半径之比、线速度之比都等于质量之反比.(2)设二者质量分别为 和
和 ,二者相距L,试写出它们角速度的表达式.
,二者相距L,试写出它们角速度的表达式.
答案:略
解析:
解析:
|
(1) 见解析;(2)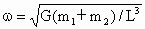 . .
两天体组成的双星做圆周运动的角速度 ω相同,二者的轨道是圆心为O的同心圆,圆的半径分别为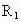 和 和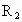 ,如图所示, ,如图所示,
(1) 证明对两天体由万有引力定律可分别列出:
由①、②得: 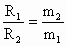 ,因为v=ωR,v∝R, ,因为v=ωR,v∝R,
所以 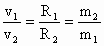 . .
(2) 由①式得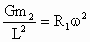 ,由②式得 ,由②式得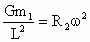 , , 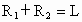 . .
故 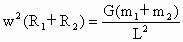
关于双星问题以及类似双星的问题,要抓住角速度相等的特点.“双星”做圆周运动的向心力是它们之间的万有引力;“双星”做圆周运动的圆心是同一圆心,半径都小于它们间的距离,它们的圆轨道半径之和等于它们间的距离. |

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目