题目内容
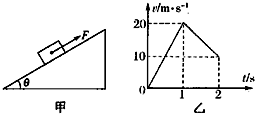如图甲所示，质量m=1.0kg的物体置于倾角θ=37°的固定粗糙斜面上，t=0时对物体施以平行于斜面向上的拉力F，t1=1s时撤去拉力，物体运动的部分v-t图象如图乙所示．设斜面足够长，物体所受最大静摩擦力与滑动摩擦力大小相等，求拉力F的大小及物块能上升的最大高度（sin37°=0.6，cos37°=0.8，g取10m/s2）分析：根据速度的斜率求出物体的加速度，由牛顿第二定律求出第1s内和第2s内物体的加速度．根据牛顿第二分别得出两段时间内F与加速度的方程，求出F．由图读出撤去拉力时物体的速度，由位移公式求出物块能上升的最大高度．
解答：解：由图象可知，撤去拉力前后物体的加速度大小分别为
a1=
=
=20m/s2，a2=
=
=10m/s2
根据牛顿第二定律得
F-μmgcosθ-mgsinθ=ma1
mgsinθ+μmgcosθ=ma2
得F=m（a1+a2）=1×1×（20+10）N=30N
撤去F前物体上滑的距离S1=
=
m=10m
S2=
=
m=20m
所以H=（s1+s2）sinθ=18m
答：拉力F的大小为30N，物块能上升的最大高度为18m．
a1=
| △v |
| △t |
| 20-0 |
| 1-0 |
| △v |
| △t |
| 20-10 |
| 2-1 |
根据牛顿第二定律得
F-μmgcosθ-mgsinθ=ma1
mgsinθ+μmgcosθ=ma2
得F=m（a1+a2）=1×1×（20+10）N=30N
撤去F前物体上滑的距离S1=
| vt1 |
| 2 |
| 20×1 |
| 2 |
S2=
| v2 |
| 2a2 |
| 202 |
| 2×10 |
所以H=（s1+s2）sinθ=18m
答：拉力F的大小为30N，物块能上升的最大高度为18m．
点评：本题首先要理解速度的物理意义：斜率等于加速度，“面积”等于位移．也可以根据动量定理和动能定理结合求解．
练习册系列答案
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案
相关题目
如图甲所示，质量m=1kg的小球放在光滑的水平面上，在界线MN的左方始终受到水平恒力F1的作用，在MN的右方除受F1外还受到与F1在同条直线上的水平恒力F2的作用．小球从A点由静止开始运动，运动的v-t图象如图乙所示．由图可知，下列说法中正确的是（ ）
