题目内容
有两个光滑球，半径均为r=3cm，重均为8N，静止在半径为R=8cm的光滑半球形碗底，如图所示．两球间的相互作用力的大小为 N．当碗的半径增大时，两球间的相互作用力变 ，球对碗的压力变 （填“大”或“小”）．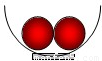
【答案】分析：以左侧小球为研究对象，分析受力情况可知：重力G、碗的支持力N和另一球的弹力F，由几何知识求出N与竖直方向的夹角θ，再根据平衡条件求解F．当碗的半径增大时，θ减小，分析F和N的变化情况．
解答：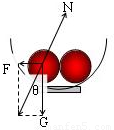
解：对左侧小球进行受力分析：重力G、碗的支持力N和另一球的弹力F．设N与竖直方向的夹角为θ，由几何知识得：sinθ=
，cosθ=
，则tanθ=
根据平衡条件得：
F=Gtanθ=8×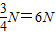
，N=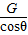
当碗的半径增大时，θ减小，由上两式得：tanθ变小，cosθ变大，则F变小，N变小，所以两球间的相互作用力变小，球对碗的压力变小．
故答案为：6，小，小．
点评：本题关键是根据几何知识求出碗对球的支持力与竖直方向的夹角，并根据平衡条件求解两球相互作用力，再讨论两力的变化．
解答：
解：对左侧小球进行受力分析：重力G、碗的支持力N和另一球的弹力F．设N与竖直方向的夹角为θ，由几何知识得：sinθ=，cosθ=，则tanθ=根据平衡条件得：
F=Gtanθ=8×
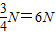，N=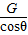当碗的半径增大时，θ减小，由上两式得：tanθ变小，cosθ变大，则F变小，N变小，所以两球间的相互作用力变小，球对碗的压力变小．
故答案为：6，小，小．
点评：本题关键是根据几何知识求出碗对球的支持力与竖直方向的夹角，并根据平衡条件求解两球相互作用力，再讨论两力的变化．
练习册系列答案
相关题目
有两个光滑球，半径均为r=3cm，重均为8N，静止在半径为R=8cm的光滑半球形碗底，如图所示．两球间的相互作用力的大小为
有两个光滑球，半径均为r＝3cm，重均为8N，静止在半径为R＝8cm的光滑半球形碗底，如图12所示。两球间的相互作用力的大小为_______N。当碗的半径增大时，两球间的相互作用力变___________，球对碗的压力变___________（填“大”或“小”）。
有两个光滑球，半径均为r＝3cm，重均为8N，静止在半径为R＝8cm的光滑半球形碗底，如图所示。两球间的相互作用力的大小为_______N。当碗的半径增大时，两球间的相互作用力变___________，球对碗的压力变___________（填“大”或“小”）。
有两个光滑球，半径均为r＝3cm，重均为8N，静止在半径为R＝8cm的光滑半球形碗底，如图所示。两球间的相互作用力的大小为_______N。当碗的半径增大时，两球间的相互作用力变___________，球对碗的压力变___________（填“大”或“小”）。