题目内容
9.两质量之比为 m1:m2=2:1 的卫星绕地球做匀速圆周运动,运动的轨道半径之比R1:R2=1:2,则下列关于两颗卫星的说法中正确的是( )| A. | 线速度大小之比为v1:v2=$\sqrt{2}$:1 | B. | 运动的周期之比为T1:T2=4:1 | ||
| C. | 向心加速度大小之比为a1:a2=4:1 | D. | 角速度之比为ω1:ω2=2:1 |
分析 已知卫星的质量和轨道半径之比,可以由万有引力提供向心力列式,分析线速度,向心加速度,周期,角速度的关系.
解答 解:A、根据万有引力等于向心力得:G$\frac{Mm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$,解得:v=$\sqrt{\frac{GM}{r}}$,已知R1:R2=1:2,代入得,两颗卫星线速度之比为v1:v2=$\sqrt{2}$:1.故A正确.
B、根据万有引力提供向心力得:G$\frac{Mm}{{r}^{2}}$=m$\frac{4{π}^{2}}{{T}^{2}}$r,解得:T=2π$\sqrt{\frac{{r}^{3}}{GM}}$,故两颗卫星周期之比为:T1:T2=1:8,故B错误.
C、根据万有引力提供向心力得:G$\frac{Mm}{{r}^{2}}$=ma,解得:a=G$\frac{M}{{r}^{2}}$,故两颗卫星的向心加速度之比为:a1:a2=4:1,故C正确.
D、根据万有引力提供向心力得:G$\frac{Mm}{{r}^{2}}$=mω2r,解得:ω=$\sqrt{\frac{GM}{{r}^{3}}}$,故两颗卫星角速度之比为:ω1:ω2=$2\sqrt{2}$:1,故D错误.
故选:AC
点评 本题重点是掌握万有引力提供向心力的各种表达形式,进而才能灵活分析各个量与半径的关系.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
19.一列沿x轴负方向传播的简谐机械横波,波速为2m/s.某时刻波形如图所示,下列说法中正确的是( )

| A. | 这列波的周期为2s | B. | 这列波的振幅为4cm | ||
| C. | 此时x=4m处质点的速度为零 | D. | 此时x=4m处质点沿y轴正方向运动 |
20.一个做简谐运动的单摆周期是1s,以下说法错误的是( )
| A. | 摆长缩短为原来的四分之一时,频率是2 Hz | |
| B. | 摆球的质量减少到原来的四分之一时,周期是4 s | |
| C. | 振幅减小为原来的四分之一时,周期是1 s | |
| D. | 如果重力加速度减小为原来的$\frac{1}{4}$时,频率是0.5 Hz |
17. 如图1所示,以v0=10m/s的水平速度抛出一物体,不计空气阻力,飞行一段时间后,垂直的撞在倾角为30°的斜面上.物体完成这段飞行的时间是( )
如图1所示,以v0=10m/s的水平速度抛出一物体,不计空气阻力,飞行一段时间后,垂直的撞在倾角为30°的斜面上.物体完成这段飞行的时间是( )
 如图1所示,以v0=10m/s的水平速度抛出一物体,不计空气阻力,飞行一段时间后,垂直的撞在倾角为30°的斜面上.物体完成这段飞行的时间是( )
如图1所示,以v0=10m/s的水平速度抛出一物体,不计空气阻力,飞行一段时间后,垂直的撞在倾角为30°的斜面上.物体完成这段飞行的时间是( )| A. | $\sqrt{3}s$ | B. | 2s | C. | $\frac{{\sqrt{3}}}{3}s$ | D. | $\frac{{2\sqrt{3}}}{3}s$ |
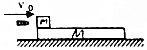 如图所示,质量为M的木板房在光滑水平面上,其左端放置一个质量为m的小滑块,开始时二者均处于静止状态,现有一质量为m0的子弹以水平速度v0击中滑块并留在其中,已知木板足够长,小滑块与木板之间的动摩擦因数为μ,求小滑块在木板上滑过的距离.
如图所示,质量为M的木板房在光滑水平面上,其左端放置一个质量为m的小滑块,开始时二者均处于静止状态,现有一质量为m0的子弹以水平速度v0击中滑块并留在其中,已知木板足够长,小滑块与木板之间的动摩擦因数为μ,求小滑块在木板上滑过的距离. 如图所示,水平面上OM正中间有质量分别为2m、m的两物块B、C(中间粘有少量炸药),现引爆炸药,B、C被水平弹开,物块C运动到O点时,与刚好到达该点、质量为m、速度大小为v0的小物块A发生迎面正碰,碰后两者结合为一体向左滑动并刚好在M点与B相碰.不计一切摩擦,不计物体碰撞时间,三物块均可视为质点,重力加速度g=10m/s2.求:
如图所示,水平面上OM正中间有质量分别为2m、m的两物块B、C(中间粘有少量炸药),现引爆炸药,B、C被水平弹开,物块C运动到O点时,与刚好到达该点、质量为m、速度大小为v0的小物块A发生迎面正碰,碰后两者结合为一体向左滑动并刚好在M点与B相碰.不计一切摩擦,不计物体碰撞时间,三物块均可视为质点,重力加速度g=10m/s2.求: 如图所示,两平行金属导轨位于同一水平面上,相距l,左端与一电阻R相连.整个系统置于匀强磁场中,磁感应强度大小为B,方向竖直向下.一质量为m的导体棒置于导轨上,在水平外力作用下沿导轨以速度v匀速向右滑动,滑动过程中始终保持与导轨垂直并接触良好.已知导体棒与导轨间的动摩擦因数为μ,重力加速度大小为g,导轨和导体棒的电阻均可忽略.求:
如图所示,两平行金属导轨位于同一水平面上,相距l,左端与一电阻R相连.整个系统置于匀强磁场中,磁感应强度大小为B,方向竖直向下.一质量为m的导体棒置于导轨上,在水平外力作用下沿导轨以速度v匀速向右滑动,滑动过程中始终保持与导轨垂直并接触良好.已知导体棒与导轨间的动摩擦因数为μ,重力加速度大小为g,导轨和导体棒的电阻均可忽略.求: