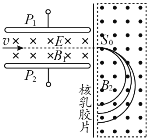
��Ŀ����
����Ŀ����ͼ������Ϊm=1 kg��С����(��Ϊ�ʵ�)�ڰ뾶ΪR=0.2 m���ķ�֮һ�⻬Բ����A���ɾ�ֹ��ʼ�ͷţ�ͨ��B���ڹ⻬ˮƽ�����˶�һ�ξ��������C��ͨ�����������ɵ����Ϊ![]() ����x=1 m��б��CD��(��C��ʱ�ٶȴ�С����) ��CDб��������������ɣ���Ħ�������ɵ���б��ײ�D����⻬����ƽ������������ͨ��D��ǰ���ٶȴ�С���䡣������һ���ᵯ��һ�˹̶���O�㣬��Ȼ״̬����һ��ǡ����D�㡣���Ħ�������ڻ���Ħ������sin37��=0.6��cos37��=0. 8�����ƿ���������
����x=1 m��б��CD��(��C��ʱ�ٶȴ�С����) ��CDб��������������ɣ���Ħ�������ɵ���б��ײ�D����⻬����ƽ������������ͨ��D��ǰ���ٶȴ�С���䡣������һ���ᵯ��һ�˹̶���O�㣬��Ȼ״̬����һ��ǡ����D�㡣���Ħ�������ڻ���Ħ������sin37��=0.6��cos37��=0. 8�����ƿ���������

(1)��ͨ��B��ʱ�Թ����ѹ����С;
(2)��CD���뻬���Ķ�Ħ��������=7/16�����ʵ��C�˶���D��ʱ��;
(3)����������ͣ��D�㣬��CD��Ħ��������ȡֵ��Χ��
���𰸡���1��![]() ��2��t= 0.4s ��3��
��2��t= 0.4s ��3��![]() ��
��![]()
��������
(1) ��A��B�ɻ�е���غ�:
![]()
���
v1=2m/s
��B����ţ�ٵڶ�����:
![]()
��:
FB= 30N
��ţ�ٵ������ɵû���Թ����ѹ��FB= 30N
(2)��б������ţ�ٵڶ�����:
![]()
���:
a=2 5m/s2
���˶�ѧ��ʽ:
![]()
���:
t= 0.4s
(3)��������ͣ��D�������ֿ���
a.����ǡ���ܴ�C�㻬��D�㣬����:
![]()
�����: ![]()
b.������б��CD��ˮƽ������η����˶������վ�ֹ��D�㡣
![]()
���
![]()
���ϣ�����ȡֵ��ΧΪ![]() ��
��![]()
�𰸣���1��![]() ��2��t= 0.4s ��3��
��2��t= 0.4s ��3��![]() ��
��![]()

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�