��Ŀ����
����Ŀ����ͼ���������l�Ĺ⻬ƽ�н�������λ��ͬһˮƽ�棨ֽ�棩�ڣ�����˽�һ��ֵΪR�ĵ��裻һ�뵼�촹ֱ�Ľ����������������ϣ��ڵ��衢����ͽ������м���һ���ΪS�����������д��ڴ�ֱ��ֽ������ľ��ȴų����Ÿ�Ӧǿ�ȴ���B1��ʱ��t�ı仯��ϵΪ ![]() ��ʽ��kΪ�������ڽ������Ҳ��һ��ǿ�ų�����������߽�MN�����ߣ��뵼�촹ֱ���ų��ĴŸ�Ӧǿ�ȴ�СΪB0 �� ����Ҳ��ֱ��ֽ�����ijʱ�̣���������һ���ˮƽ�����������´Ӿ�ֹ��ʼ�����˶�����t0ʱ��ǡ�����ٶ�v0Խ��MN���˺������������˶����������뵼��ʼ�����ֱ���Ӵ����ã����ǵĵ�������Բ��ơ���
��ʽ��kΪ�������ڽ������Ҳ��һ��ǿ�ų�����������߽�MN�����ߣ��뵼�촹ֱ���ų��ĴŸ�Ӧǿ�ȴ�СΪB0 �� ����Ҳ��ֱ��ֽ�����ijʱ�̣���������һ���ˮƽ�����������´Ӿ�ֹ��ʼ�����˶�����t0ʱ��ǡ�����ٶ�v0Խ��MN���˺������������˶����������뵼��ʼ�����ֱ���Ӵ����ã����ǵĵ�������Բ��ơ���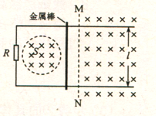
��1����t=0��t=t0ʱ�����ڣ���������ĵ�����ľ���ֵ��
��2����ʱ��t��t>t0��������·���ܴ�ͨ���ͽ������������ˮƽ�����Ĵ�С��
���𰸡�
��1��
�⣺�ڽ�����δ����MN֮ǰ��tʱ�̴�����·�Ĵ�ͨ��Ϊ ![]() ��
��
���ڴ�tʱ�̵� ![]() ��ʱ�����ڣ���·��ͨ���ı仯��Ϊ
��ʱ�����ڣ���·��ͨ���ı仯��Ϊ ![]() ����������R�ĵ����Ϊ
����������R�ĵ����Ϊ ![]()
���ݷ����ڵ�Ÿ�Ӧ�� ![]() ��
��
����ŷķ���ɿɵ� ![]() ��
��
���ݵ����Ķ���ɵ� ![]() ��
��
�����٢ڢۢܿɵ� ![]() �ݸ��ݢݿɵ���t=0��t=
�ݸ��ݢݿɵ���t=0��t= ![]() ��ʱ�����ڣ���������R�ĵ����q�ľ���ֵΪ
��ʱ�����ڣ���������R�ĵ����q�ľ���ֵΪ ![]() ��
��
����������ĵ�����ľ���ֵΪ ![]()
��2��
�⣺�� ![]() ʱ����������Խ��MN�����ڽ�������MN�Ҳ��������˶�����
ʱ����������Խ��MN�����ڽ�������MN�Ҳ��������˶����� ![]() ��
��
ʽ��f�����ˮƽ������F����ǿ�ų�ʩ�ӵİ����������ʱ��·�еĵ���ΪI��F�Ĵ�СΪ ![]() ��
��
��ʱ��������MN֮��ľ���Ϊ ![]() ��
��
��ǿ�ų�������·�Ĵ�ͨ��Ϊ ![]()
��·���ܴ�ͨ��Ϊ ![]()
ʽ�� ![]() �����ʽ��ʾ���ɢ٢���ɵ���ʱ��t��
�����ʽ��ʾ���ɢ٢���ɵ���ʱ��t�� ![]() ��������·���ܴ�ͨ��Ϊ
��������·���ܴ�ͨ��Ϊ ![]()
��t�� ![]() ��ʱ�����ڣ��ܴ�ͨ���ĸı�
��ʱ�����ڣ��ܴ�ͨ���ĸı� ![]() Ϊ
Ϊ ![]()
�ɷ����ڵ�Ÿ�Ӧ���ɿɵã���Ӧ�綯�ƵĴ�СΪ ![]()
��ŷķ������ ![]()
�����ߢ��ɵ� ![]()
����ʱ��t��t>t0��������·���ܴ�ͨ���ͽ������������ˮƽ�����Ĵ�СΪ ![]()
����������1�����ݷ����ڵ�Ÿ�Ӧ���ɣ���ϱպϵ�·ŷķ���ɣ�����������ʽ���Ӷ������������ۺϱ���ʽ��������⣻��2�����ݴ�ͨ���ĸ��=BS����ϴų�������������·���ܴ�ͨ�������ݶ����綯��������綯�ƹ�ʽ�������Ȧ�е��ܸ�Ӧ�綯�ƣ������ݱպϵ�·ŷķ���ɣ�������������ʽ���������ƽ���������������ˮƽ������С��
�����㾫����������Ĺؼ����������Ÿ�Ӧ��������֪ʶ�����յ�Ÿ�Ӧ�����ʵ���Dz�����Ӧ�綯�ƣ������·�պϣ����и�Ӧ��������·���պϣ���ֻ�и�Ӧ�綯�ƶ���Ӧ������