题目内容
如图,一个很长的竖直放置的圆柱形磁铁,产生一个辐射状的磁场(磁场水平向外),其大小为B=K/r,r为半径,设一个与磁铁同轴的圆形铝环,半径为R(大于圆柱形磁铁半径),而弯成铝环的铝丝其截面积为S,铝丝电阻率为ρ,密度为ρ.铝环通过磁场由静止开始下落,下落过程中铝环平面始终保持水平.试求:(1)铝环下落速度为v时的电功率?
(2)铝环下落的最终速度?
(3)当下落h高度时,速度最大,此过程中圆环消耗的电能?

【答案】分析:(1)根据电阻定律求出圆环的电阻,根据法拉第电磁感应定律求出切割磁感线产生的电动势,根据电功率的表达式求解.
(2)当圆环加速度为零时,有最大速度,由平衡条件求解.
(3)由能量守恒定律求解.
解答:解:(1)由题意知圆环所在处的磁感应强度B= ,圆环的有效切割长度为其周长,即L=2πR,
,圆环的有效切割长度为其周长,即L=2πR,
圆环的电阻R= =
= ,当圆环的速度为v时,切割磁感线产生的电动势E=BLv=2kπv,
,当圆环的速度为v时,切割磁感线产生的电动势E=BLv=2kπv,
圆环中的电流I= ,圆环速度为v时电功率P=I2R
,圆环速度为v时电功率P=I2R
联立以上各式解得:P=
(2)当圆环加速度为零时,有最大速度vm,此时安培力F=BIL=
由平衡条件可知:mg=F,圆环的质量m=ρS?2πR
解得:vm=
(3)由能量守恒定律得:
mgh= m
m +Q
+Q
解得:Q=2πρRS[gh- (
( )2]
)2]
答:(1)铝环下落速度为v时的电功率是
(2)铝环下落的最终速度是
(3)当下落h高度时,速度最大,此过程中圆环消耗的电能是2πρRS[gh- (
( )2].
)2].
点评:解决该题关键是把电磁感应与电路知识,能量守恒定律结合起来求解.
(2)当圆环加速度为零时,有最大速度,由平衡条件求解.
(3)由能量守恒定律求解.
解答:解:(1)由题意知圆环所在处的磁感应强度B=
 ,圆环的有效切割长度为其周长,即L=2πR,
,圆环的有效切割长度为其周长,即L=2πR,圆环的电阻R=
 =
= ,当圆环的速度为v时,切割磁感线产生的电动势E=BLv=2kπv,
,当圆环的速度为v时,切割磁感线产生的电动势E=BLv=2kπv,圆环中的电流I=
 ,圆环速度为v时电功率P=I2R
,圆环速度为v时电功率P=I2R 联立以上各式解得:P=

(2)当圆环加速度为零时,有最大速度vm,此时安培力F=BIL=

由平衡条件可知:mg=F,圆环的质量m=ρS?2πR
解得:vm=

(3)由能量守恒定律得:
mgh=
 m
m +Q
+Q 解得:Q=2πρRS[gh-
 (
( )2]
)2]答:(1)铝环下落速度为v时的电功率是

(2)铝环下落的最终速度是

(3)当下落h高度时,速度最大,此过程中圆环消耗的电能是2πρRS[gh-
 (
( )2].
)2].点评:解决该题关键是把电磁感应与电路知识,能量守恒定律结合起来求解.

练习册系列答案
相关题目
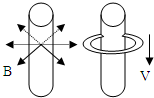 (2009?青浦区一模)如图,一个很长的竖直放置的圆柱形磁铁,产生一个辐射状的磁场(磁场水平向外),其大小为B=K/r,r为半径,设一个与磁铁同轴的圆形铝环,半径为R(大于圆柱形磁铁半径),而弯成铝环的铝丝其截面积为S,铝丝电阻率为ρ,密度为ρ0.铝环通过磁场由静止开始下落,下落过程中铝环平面始终保持水平.试求:
(2009?青浦区一模)如图,一个很长的竖直放置的圆柱形磁铁,产生一个辐射状的磁场(磁场水平向外),其大小为B=K/r,r为半径,设一个与磁铁同轴的圆形铝环,半径为R(大于圆柱形磁铁半径),而弯成铝环的铝丝其截面积为S,铝丝电阻率为ρ,密度为ρ0.铝环通过磁场由静止开始下落,下落过程中铝环平面始终保持水平.试求:
