题目内容
 如图所示,A、B、C三个木块的质量均为m,置于光滑的水平桌面上.B、C之间有一轻质弹簧,弹簧的两端与木块B、C牢固连接,弹簧处于原长.现A以初速v0沿B、C的连线方向朝B运动,与B相碰并粘合在一起.求:
如图所示,A、B、C三个木块的质量均为m,置于光滑的水平桌面上.B、C之间有一轻质弹簧,弹簧的两端与木块B、C牢固连接,弹簧处于原长.现A以初速v0沿B、C的连线方向朝B运动,与B相碰并粘合在一起.求:(1)A、B相碰后瞬间的速度大小;
(2)三个木块最终的速度大小;
(3)弹簧中能达到的最大弹性势能.
分析:(1)A、B碰撞的瞬间,A、B组成的系统动量守恒,C认为未参与碰撞,根据动量守恒定律求出碰后瞬间AB的速度;
(2)、(3)当三种速度相同时,弹簧压缩到最短,弹性势能最大,根据三个物体组成的动量守恒定律和能量守恒定律求出三个木块最终的速度大小和弹簧的最大弹性势能.
(2)、(3)当三种速度相同时,弹簧压缩到最短,弹性势能最大,根据三个物体组成的动量守恒定律和能量守恒定律求出三个木块最终的速度大小和弹簧的最大弹性势能.
解答:解:(1)设碰后A、B共同速度的大小为v1,由动量守恒得:
mv0=2mv1 ①
解得A、B相碰后瞬间的速度大小为
v0
(2)设A、B、C的最终的速度大小为v2,由动量守恒得:
mv0=3mv2 ②
解得A、B、C最终的速度大小为
v0
(3)设弹簧的最大弹性势能为Ep,A、B相碰后机械能守恒,有
(2m)v
=
(3m)v22+Ep ③
联立①②③式解得:Ep=
mv
答:(1)A、B相碰后瞬间的速度大小为
v0;(2)三个木块最终的速度大小为
v0;(3)弹簧中能达到的最大弹性势能为
mv
.
mv0=2mv1 ①
解得A、B相碰后瞬间的速度大小为
| 1 |
| 2 |
(2)设A、B、C的最终的速度大小为v2,由动量守恒得:
mv0=3mv2 ②
解得A、B、C最终的速度大小为
| 1 |
| 3 |
(3)设弹簧的最大弹性势能为Ep,A、B相碰后机械能守恒,有
| 1 |
| 2 |
2 1 |
| 1 |
| 2 |
联立①②③式解得:Ep=
| 1 |
| 12 |
2 0 |
答:(1)A、B相碰后瞬间的速度大小为
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 12 |
2 0 |
点评:本题综合考查了动量守恒定律和能量守恒定律,综合性较强,对学生的能力要求较高,要加强这方面的训练.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目

 如图所示,a、b、c为电场中同一电场线上的三点,且b为ac的中点,a、c电势分别为φa=8V,φc=6V.下列叙述正确的是( )
如图所示,a、b、c为电场中同一电场线上的三点,且b为ac的中点,a、c电势分别为φa=8V,φc=6V.下列叙述正确的是( ) 如图所示,A、B、C、D是某匀强电场中的4个等势面,一个质子和一个α粒子(电荷量是质子的2倍,质量是质子的4倍)同时在A等势面从静止出发,向右运动,当到达D等势面时,下列说法正确的是( )
如图所示,A、B、C、D是某匀强电场中的4个等势面,一个质子和一个α粒子(电荷量是质子的2倍,质量是质子的4倍)同时在A等势面从静止出发,向右运动,当到达D等势面时,下列说法正确的是( ) 如图所示,a、b和c都是厚度均匀的平玻璃板,a和b、b和c之间的夹角都为α,一细光束由红光和蓝光组成,以入射角θ从O点射入a板,且射出c板后的两束单色光通过空气射在地面上P、Q两点,由此可知( )
如图所示,a、b和c都是厚度均匀的平玻璃板,a和b、b和c之间的夹角都为α,一细光束由红光和蓝光组成,以入射角θ从O点射入a板,且射出c板后的两束单色光通过空气射在地面上P、Q两点,由此可知( )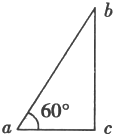 如图所示,a、b、c是匀强电场中的直角三角形的三个顶点.已知a、b、c三点的电势分别为φa=8V、φb=-4V、φc=2V,
如图所示,a、b、c是匀强电场中的直角三角形的三个顶点.已知a、b、c三点的电势分别为φa=8V、φb=-4V、φc=2V,