题目内容
(9分)如图,一质量为m的平板车左端放有质量为M的小滑块,滑块与平板车之间的动摩擦因数为μ。开始时,平板车和滑块共同以速度v0沿光滑水平面向右运动,并与竖直墙壁发生碰撞,设碰撞时间极短,且碰撞后平板车速度大小保持不变,但方向与原来相反。平板车足够长,以至滑块不会滑出平板车右端,重力加速度为g。求
①平板车第一次与墙壁碰撞后再次与滑块速度相同时两者的共同速度;
②平板车第一次与墙壁碰撞后再次与滑块速度相同时,平板车右端距墙壁的距离。
①v= v0,②
v0,②
解析试题分析:①设共同速度为v,由动量守恒
Mv0-mv0=(M+m)v (2分)
所以,v= v0 (2分)
v0 (2分)
②设小车与墙碰撞后向左运动的最大距离为x1
与墙碰撞后小车从左侧最远处运动到与滑块具有共同速度时通过的距离为x2
由动能定理
-μMg x1="0" -  mv
mv (2分)
(2分)
μMg x2= mv
mv (2分)
(2分)
所以,所求平板车右端距墙壁的距离为
Δx= x1 - x2= (1分)
(1分)
考点:本题考查了动量守恒定律的应用

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
如图所示一长为 、质量为
、质量为 的车厢静止于光滑水平面上,车厢内有—质量为
的车厢静止于光滑水平面上,车厢内有—质量为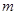 的物体以初速度
的物体以初速度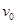 向右运动,与车厢来回碰撞
向右运动,与车厢来回碰撞 次后静止于车厢中,这时车厢的速度为( )
次后静止于车厢中,这时车厢的速度为( )
A.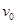 ,水平向右 ,水平向右 | B.零 |
C. , 水平向右 , 水平向右 | D. ,水平向右 ,水平向右 |
如图所示,小车与木箱紧挨着静放在光滑的水平冰面上,现有一男孩站在小车上用力向右迅速推出木箱,关于上述过程,下列说法中正确的是( )
| A.男孩和木箱组成的系统动量守恒 |
| B.男孩、小车与木箱三者组成的系统动量守恒 |
| C.小车与木箱组成的系统动量守恒 |
| D.木箱的动量增量与男孩、小车的总动量增量相同 |
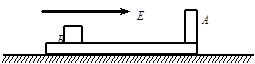
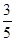 ,碰撞时间极短,则碰撞后滑板速度多大?(均指对地速度)
,碰撞时间极短,则碰撞后滑板速度多大?(均指对地速度)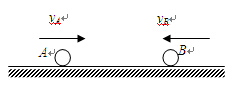
 vB C.vA=
vB C.vA=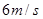 ,B球的速度是
,B球的速度是 ,不久A、B两球发生了对心碰撞。对于该碰撞之后的A、B两球的速度可能值,某实验小组的同学们做了很多种猜测,下面的哪一种猜测结果一定无法实现的是( )
,不久A、B两球发生了对心碰撞。对于该碰撞之后的A、B两球的速度可能值,某实验小组的同学们做了很多种猜测,下面的哪一种猜测结果一定无法实现的是( )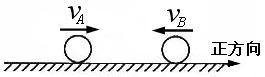
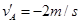 ,
,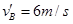 B.
B.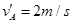 ,
,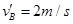
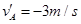 ,
, D.
D. ,
,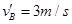
 ,现用大小相等的两个力F1和F2分别作用在A和B上,使A、B沿一条直线相向运动,然后又先后撤去这两个力,使这两个物体具有相同的动能,接着两物体碰撞并合为一体后,它们
,现用大小相等的两个力F1和F2分别作用在A和B上,使A、B沿一条直线相向运动,然后又先后撤去这两个力,使这两个物体具有相同的动能,接着两物体碰撞并合为一体后,它们






 ,碰撞前后打出的纸带如图(b)所示。
,碰撞前后打出的纸带如图(b)所示。
 最大为5℅,本实验是否在误差范围内验证了动量守恒定律?写出运算过程。
最大为5℅,本实验是否在误差范围内验证了动量守恒定律?写出运算过程。