题目内容
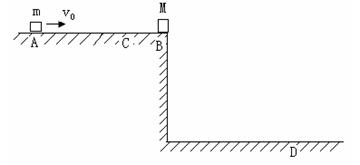
如图所示,一质量为![]() 的长木板静止在水平面上,有一质量为
的长木板静止在水平面上,有一质量为![]() 的小滑块以一定的水平速度冲上木板,已知滑块和木板之间的动摩擦因数为
的小滑块以一定的水平速度冲上木板,已知滑块和木板之间的动摩擦因数为![]() ,最大静摩擦力等于滑动摩擦力,求:
,最大静摩擦力等于滑动摩擦力,求:
(1)若滑块在木板上滑动时,木板能保持静止不动,木板和地面之间的动摩擦因数须满足什么条件?
(2)若长木板的质量![]() ,长木板与水平面间的动摩擦因数
,长木板与水平面间的动摩擦因数![]() .滑块的质量也为
.滑块的质量也为![]() .滑块以
.滑块以![]() 的速度滑上长木板的左端,小滑块与长木板间的动摩擦因数
的速度滑上长木板的左端,小滑块与长木板间的动摩擦因数![]() .滑块最终没有滑离长木板,求滑块在开始滑上长木板到最后静止下来的过程中,滑块滑行的距离是多少?(
.滑块最终没有滑离长木板,求滑块在开始滑上长木板到最后静止下来的过程中,滑块滑行的距离是多少?(![]() )
)
解:
(1)长木板受到滑块向前的摩擦力![]()
设长木板与地面之间的动摩擦因数为![]()
长木板受到地面的最大静摩擦力大小![]()
由题意得:![]()
![]()
![]()
即:![]()
![]()
![]()
(2)对![]() :
:![]() 解得:
解得:![]()
对![]() :
:![]() 解得:
解得:![]()
设经历时间为![]() 两者速度相同,则:
两者速度相同,则:![]()
解得:![]()
两者共同速度为:![]()
两者相对静止前,小滑块的位移:![]()
达到共同速度后对滑块和木板:![]() 解得:
解得:![]()
滑行位移为:![]() 解得:
解得:![]()
小滑块的总位称为:![]()

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 的物块A与直立轻弹簧的上端连接,弹簧的下端固定在地面上,一质量也为
的物块A与直立轻弹簧的上端连接,弹簧的下端固定在地面上,一质量也为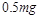 时,A物块上升的高度为L,此过程中,该拉力做的功为
时,A物块上升的高度为L,此过程中,该拉力做的功为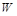 ;若A、B不粘连,用一竖直向上的恒力
;若A、B不粘连,用一竖直向上的恒力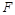 作用在B上,当A物块上升的高度也为L时,A、B恰好分离。已知重力加速度为g,不计空气阻力,求:
作用在B上,当A物块上升的高度也为L时,A、B恰好分离。已知重力加速度为g,不计空气阻力,求: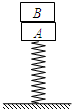
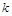 ;
;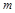 的物块A与直立轻弹簧的上端连接,弹簧的下端固定在地面上,一质量也为
的物块A与直立轻弹簧的上端连接,弹簧的下端固定在地面上,一质量也为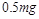 时,A物块上升的高度为L,此过程中,该拉力做的功为
时,A物块上升的高度为L,此过程中,该拉力做的功为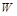 ;若A、B不粘连,用一竖直向上的恒力
;若A、B不粘连,用一竖直向上的恒力 作用在B上,当A物块上升的高度也为L时,A、B恰好分离。已知重力加速度为g,不计空气阻力,求:
作用在B上,当A物块上升的高度也为L时,A、B恰好分离。已知重力加速度为g,不计空气阻力,求: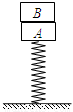
 ;
;