题目内容
 （2010?重庆）如图所式，矩形MNPQ区域内有方向垂直于纸面的匀强磁场，有5个带点粒子从图中箭头所示位置垂直于磁场边界进入磁场，在纸面内做匀速圆周运动，运动轨迹为相应的圆弧，这些粒子的质量，电荷量以及速度大小如下表所示．由以上信息可知，从图中abc处进入的粒子对应表中的编号分别为（ ）
|
分析：带电粒子在磁场中的运动洛仑兹力充当向心力，由此可得出半径公式，由半径公式可得出各组粒子的半径之比；则可得出它们的运动轨迹．
解答：解：由Bqv=m
可知，半径公式r=
；
结合表格中数据可求得1-5各组粒子的半径之比依次为0.5：2：3：3：2，说明第一组正粒子的半径最小，由图可知故该粒子从MQ边界进入磁场逆时针运动．
由图a、b粒子进入磁场也是逆时针运动，则都为正电荷，而且a、b粒子的半径比为2：3，则a一定是第2组粒子，b是第4组粒子．c顺时针运动，都为负电荷，半径与a相等是第5组粒子．
故选D．
| v2 |
| r |
| mv |
| Bq |
结合表格中数据可求得1-5各组粒子的半径之比依次为0.5：2：3：3：2，说明第一组正粒子的半径最小，由图可知故该粒子从MQ边界进入磁场逆时针运动．
由图a、b粒子进入磁场也是逆时针运动，则都为正电荷，而且a、b粒子的半径比为2：3，则a一定是第2组粒子，b是第4组粒子．c顺时针运动，都为负电荷，半径与a相等是第5组粒子．
故选D．
点评：本题看似比较复杂，但只要认真分析即可发现半径大小以及偏转方向的关系，则根据带电粒子圆周运动的性质可得出正确结果．
练习册系列答案
相关题目
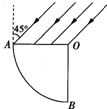（2010?重庆）如图所示，空气中有一折射率为
（2010?重庆模拟）在如图所示的电路中，灯泡L的电阻大于电源的内阻r，闭合电键s，当滑动变阻器在如图所示位置时，灯泡L能发光，若将滑动变阻器滑片P向左移动一段距离后，下列说法正确的是（ ）
（2010?重庆模拟）如图所示，沿波的传播方向上有间距均为1m的质点a、b，静止在各自的平衡位置c一列横波以1m/s的速度水平向右传播．t=0时质点a开始由平衡位置向上运动，t=1s时质点a第一次到达最高点．在4s＜t＜5s这段时间内质点c（ ）
（2010?重庆模拟）如图所示，光滑平行的金属导轨MN、PQ相距L=0.8m，其框架平面与水平面成．θ=30°，在M点和P点间接一个阻值为R=1.80Ω的电阻，在两一导轨间矩形区域00101′0′内有垂直导轨平面向下、宽为d=0.6m的匀强磁场，磁感应强度为B=lT．一质量为m=0.16kg、电阻为r=0.2Ω的导体棒ab，垂直搁置于导轨上，与磁场上边界相距d0=0.4m，现使它由静止开始运动，在棒ab离开磁场前已经做匀速直线运动（棒ab与导轨始终保持良好的接触，导轨电阻不计，g=l0m/s2）求：