题目内容
如图，动摩擦系数为u的粗糙斜面的倾角α，在斜面上放置一矩形线框abcd，ab边的边长l1bc边的边长l2，线框的质量m 电阻R，线框通过细线与重物相连，重物质量M，斜面上ef线（ef∥gh）的右方有垂直斜面向上的匀强磁场，磁感应强度B．释放M，线框从静止开始沿斜面向上运动，进入磁场最初一段时间是匀速的，ef线和gh的距离s 且s大于2l2，下列说法正确的是．（ ）分析：由题，线框刚进入磁场的过程做匀速运动，根据平衡条件求解绳子的拉力大小．线框进入磁场前，根据牛顿第二定律求解加速度．由平衡条件求出线框匀速运动的速度，可求出线框由静止开始到运动到gh线处所用的时间．M的重力势能减小转化为m的重力势能和线框中的内能，根据能量守恒定律求解焦耳热．
解答：解：A、线框进入磁场的过程做匀速运动，根据平衡条件得：绳的拉力 T=mgsinα+F安，绳子的拉力T不一定大于mg，故A错误．
B、线框进入磁场前，根据牛顿第二定律得：加速度为 a=
．
设线框匀速运动的速度大小为v，则线框受到的安培力大小为F=
，根据平衡条件得：F=Mg-mgsinα，联立可求得v．
根据运动学公式v=at，所以可求出线框由静止开始到运动到gh线处所用的时间．故B正确．
C、根据能量转化和守恒定律得知，M的重力势能减小转化为m的重力势能和线框中的内能，故C错误．
D、根据能量守恒定律得：线框由静止开始到运动到gh线的整个过程中产生的焦耳热等于系统机械能的减少，故D正确．
故选：BD
B、线框进入磁场前，根据牛顿第二定律得：加速度为 a=
| Mg-mgsinα |
| M+m |
设线框匀速运动的速度大小为v，则线框受到的安培力大小为F=
B2
| ||
| R |
根据运动学公式v=at，所以可求出线框由静止开始到运动到gh线处所用的时间．故B正确．
C、根据能量转化和守恒定律得知，M的重力势能减小转化为m的重力势能和线框中的内能，故C错误．
D、根据能量守恒定律得：线框由静止开始到运动到gh线的整个过程中产生的焦耳热等于系统机械能的减少，故D正确．
故选：BD
点评：本题是电磁感应与力平衡的综合，安培力的计算是关键．本题中运用的是整体法求解加速度．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
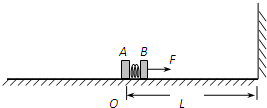（2011?湖北模拟）如图所示，水平面O点的右侧光滑，左侧粗糙．O点到右侧竖直墙壁的距离为L，一系统由可看作质点的A、B两木块和一短而硬（即劲度系数很大）的轻质弹簧构成．A，B两木块的质量均为m，弹簧夹在A与B之间，与二者接触而不固连．让A、B压紧弹簧，并将它们锁定，此时弹簧的弹性势能为E0该系统在O点从静止开始在水平恒力F作用下幵始向右运动，当运动到离墙S=L/4时撤去恒力F，撞击墙壁后以原速率反弹，反弹后当木块A运动到O点前解除锁定．通过遥控解除锁定时，弹簧可瞬时恢复原长．求
，在斜面上放置一矩形线框abcd，ab边的边长l1bc边的边长l2，线框的质量m 电阻R ，线框通过细线与重物相连，重物质量M ，斜面上ef线（ef∥gh）的右方有垂直斜面向上的匀强磁场，磁感应强度B .释放M，线框从静止开始沿斜面向上运动，进入磁场最初一段时间是匀速的，ef线和gh的距离s 且s大于2l2 ，下列说法正确的是。