题目内容
天宫一号于2011年9月29日成功发射，它将和随后发射的神州飞船在空间完成交会对接，实现中国载人航天工程的一个新的跨越．天宫一号进入运行轨道后，其运行周期为T，距地面的高度为h，已知地球半径为R，万有引力常量为G．若将天宫一号的运行轨道看做圆轨道，求：（1）地球质量M；
（2）地球的平均密度．
【答案】分析：（1）地球对天宫一号的万有引力提供它绕地球做匀速圆周运动的向心力，由万有引力公式及向心力公式列方程，可以求出地球的质量．
（2）求出地球的质量，然后由密度公式可以求出地球的密度．
解答：解：（1）天宫一号的轨道半径r=R+h，
天宫一号做圆周运动所需向心力由万有引力提供，
设天宫一号的质量是m，地球的质量是M，
由牛顿第二定律可得：G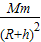
=m（
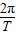）2（R+h），
地球质量M=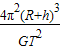
；
（2）地球的平均密度：
ρ=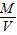
=
=
；
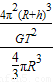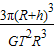答：（1）地球质量M=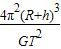
．
（2）地球的平均密度是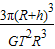
．
点评：知道万有引力提供向心力，由牛顿第二定律列方程即可求出地球质量，已知质量，由密度公式可以求出地球的平均密度．
（2）求出地球的质量，然后由密度公式可以求出地球的密度．
解答：解：（1）天宫一号的轨道半径r=R+h，
天宫一号做圆周运动所需向心力由万有引力提供，
设天宫一号的质量是m，地球的质量是M，
由牛顿第二定律可得：G
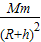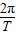=m（）2（R+h），地球质量M=
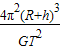；（2）地球的平均密度：
ρ=
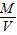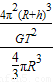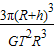==；答：（1）地球质量M=
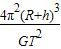．（2）地球的平均密度是
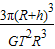．点评：知道万有引力提供向心力，由牛顿第二定律列方程即可求出地球质量，已知质量，由密度公式可以求出地球的平均密度．
练习册系列答案
相关题目
“天宫一号”于2011年9月29日21时16分3秒在酒泉卫星中心成功发射．“天宫一号”能在离地面约343km高的近圆轨道上正常运行，2011年11月14日“天宫一号”与“神舟八号”飞船成功地完成了对接试验．下列说法中正确的是（ ）