题目内容
第一个粒子质量是m1,以v0的速度与原来静止的质量为m2的第二个粒子发生一维碰撞.测出了碰撞后第二个粒子的速度为v2,求第一个粒子原来速度v0的值可能范围.
【答案】

【解析】
试题分析:本题考查动量守恒定律的特殊形式——碰撞.我们通过分析碰撞的几种形式,对碰撞中能量的转化分析清楚,本题就迎刃而解了.
m1v0=(m1+m2)v2所以v0=
这里的v0是机械能损失最大情况的值,是v0的上限,应满足v0≤ ①
①
机械能损失最小的情况是两粒子发生弹性碰撞时机械能损失为零
由m1v0=m1v1+m2v2
 m1v02=
m1v02= m1v12+
m1v12+ m2v22
m2v22
联立以上两式得v0=
得到的表达式是v0的下限,但它不符合题意,题中机械能有损失,所以v0应取为
v0> ②
②
由两式①②得 .
.
考点:动量守恒 机械能守恒 能量守恒
点评:①此题应用的解题方法可以归纳为“条件法”,特点是利用v0的端值条件与题目中给出的条件相比较决定对v0的取值.②在解题时,把完全弹性碰撞和完全非弹性碰撞,看成一般碰撞的特例,由碰撞的特点知,当碰撞后两粒子发生完全非弹性碰撞时,机械能损失最大. 即m1v0=(m1+m2)v2所以v0=

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
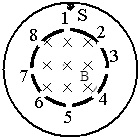 如图,两个共轴的圆筒形金属电极,在内筒上均匀分布着平行于轴线的标号1-8的八个狭缝,内筒内半径为R,在内筒之内有平行于轴线向里的匀强磁场,磁感应强度为B.在两极间加恒定电压,使筒之间的区域内有沿半径向里的电场.不计粒子重力,整个装置在真空中,粒子碰到电极时会被电极吸收.
如图,两个共轴的圆筒形金属电极,在内筒上均匀分布着平行于轴线的标号1-8的八个狭缝,内筒内半径为R,在内筒之内有平行于轴线向里的匀强磁场,磁感应强度为B.在两极间加恒定电压,使筒之间的区域内有沿半径向里的电场.不计粒子重力,整个装置在真空中,粒子碰到电极时会被电极吸收.