题目内容
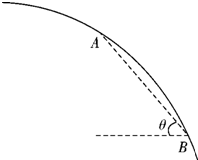（2011?武汉模拟）如图所示，一质点做平抛运动先后经过A、B两点，到达A点时速度方向与水平方向的夹角为30°，到达B点时速度方向与水平方向的夹角为60°．（1）求质点在A、B位置的竖直分速度大小之比；
（2）设质点的位移
. | AB |
分析：（1）已知速度与水平方向的夹角，则可将速度分解得出水平速度和竖直速度间的关系，即可求得竖直分速度度大小之比；
（2）AB为质点运动的水平位移和竖直位移的合位移，分别求得两位移，由几何关系即可求得tanθ的值．
（2）AB为质点运动的水平位移和竖直位移的合位移，分别求得两位移，由几何关系即可求得tanθ的值．
解答：解：
（1）设质点平抛的初速度为v0，在A、B点的竖直分速度分别为vAy、vBy，
则vAy=v0tan30°
vBy=v0tan60°
解得
=
．
（2）设从A到B时间为t，竖直位移和水平位移分别为y、x，
则tanθ=
x=v0t
y=
t
联立解得 tanθ=
．
（1）设质点平抛的初速度为v0，在A、B点的竖直分速度分别为vAy、vBy，
则vAy=v0tan30°
vBy=v0tan60°
解得
| vAy |
| vBy |
| 1 |
| 3 |
（2）设从A到B时间为t，竖直位移和水平位移分别为y、x，
则tanθ=
| y |
| x |
x=v0t
y=
| vAy+vBy |
| 2 |
联立解得 tanθ=
2
| ||
| 3 |
点评：我们平常求的位移一般都是从抛出点开始的，而本题较为新颖，选取本间一段位移进行计算，因此要注意竖直分位移的求法，本题采用了平均速度公式进行的计算，应注意体会．
练习册系列答案
相关题目
（2011?武汉模拟）如图所示，S1、S2为水波槽中的两个波源，它们分别激起两列水波，图中实线表示波峰、虚线表示波谷．已知两列波的波长λ1＜λ2，该时刻在P点为两列波的波峰与波峰相遇，则以下叙述正确的是（ ）
（2011?武汉模拟）如图所示，质量分别为m1、m2的两个物体通过轻弹簧连接，在力F的作用下一起沿水平方向做匀加速直线运动（m1在光滑地面上，m2在空中），力F与水平方向的夹角为θ．则m1的加速度大小为（ ）