题目内容
在半径为R的半圆形区域中有一匀强磁场,磁场的方向垂直于纸面,磁感应强度为B.一质量为m,带有电量q的粒子以一定的速度沿垂直于半圆直径AD方向经P点(AP=d)射入磁场(不计重力影响).(1)如果粒子恰好从A点射出磁场,求入射粒子的速度.
(2)如果粒子经纸面内Q点从磁场中射出,出射方向与半圆在Q点切线方向的夹角为φ(如图).求入射粒子的速度.
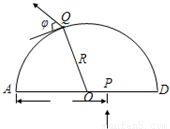
【答案】分析:(1)由于粒子在P点垂直射入磁场,故圆弧轨道的圆心在AP上,AP是直径,根据洛伦兹力提供向心力公式即可求解速度;
(2)设O′是粒子在磁场中圆弧轨道的圆心,连接O′Q,设O′Q=R′,根据几何关系即余弦定理即可求得R′,再根据洛伦兹力提供向心力公式即可求解速度;
解答:解: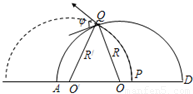 (1)由于粒子在P点垂直射入磁场,故圆弧轨道的圆心在AP上,AP是直径.
(1)由于粒子在P点垂直射入磁场,故圆弧轨道的圆心在AP上,AP是直径.
设入射粒子的速度为v1,由洛伦兹力的表达式和牛顿第二定律得: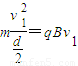
解得: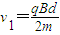
(2)设O′是粒子在磁场中圆弧轨道的圆心,连接O′Q,设O′Q=R′.
由几何关系得:∠OQO′=φ OO′=R′+R-d
由余弦定理得: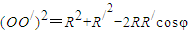
解得: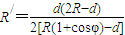
设入射粒子的速度为v,由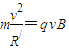
解出: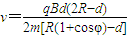
答:(1)如果粒子恰好从A点射出磁场,入射粒子的速度为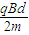 .
.
(2)如果粒子经纸面内Q点从磁场中射出,出射方向与半圆在Q点切线方向的夹角为φ(如图).入射粒子的速度为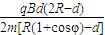 .
.
点评:熟悉电子在磁场中做匀速圆周运动由洛伦兹力提供向心力,据此列式求出半径的表达式,能正确作出粒子做圆周运动的半径.
(2)设O′是粒子在磁场中圆弧轨道的圆心,连接O′Q,设O′Q=R′,根据几何关系即余弦定理即可求得R′,再根据洛伦兹力提供向心力公式即可求解速度;
解答:解:
 (1)由于粒子在P点垂直射入磁场,故圆弧轨道的圆心在AP上,AP是直径.
(1)由于粒子在P点垂直射入磁场,故圆弧轨道的圆心在AP上,AP是直径.设入射粒子的速度为v1,由洛伦兹力的表达式和牛顿第二定律得:
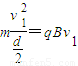
解得:
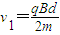
(2)设O′是粒子在磁场中圆弧轨道的圆心,连接O′Q,设O′Q=R′.
由几何关系得:∠OQO′=φ OO′=R′+R-d
由余弦定理得:
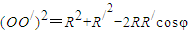
解得:
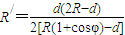
设入射粒子的速度为v,由
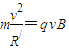
解出:
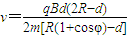
答:(1)如果粒子恰好从A点射出磁场,入射粒子的速度为
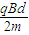 .
.(2)如果粒子经纸面内Q点从磁场中射出,出射方向与半圆在Q点切线方向的夹角为φ(如图).入射粒子的速度为
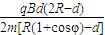 .
.点评:熟悉电子在磁场中做匀速圆周运动由洛伦兹力提供向心力,据此列式求出半径的表达式,能正确作出粒子做圆周运动的半径.

练习册系列答案
相关题目
 (2007?宁夏)在半径为R的半圆形区域中有一匀强磁场,磁场的方向垂直于纸面,磁感应强度为B.一质量为m,带有电量q的粒子以一定的速度沿垂直于半圆直径AD方向经P点(AP=d)射入磁场(不计重力影响).
(2007?宁夏)在半径为R的半圆形区域中有一匀强磁场,磁场的方向垂直于纸面,磁感应强度为B.一质量为m,带有电量q的粒子以一定的速度沿垂直于半圆直径AD方向经P点(AP=d)射入磁场(不计重力影响).


