题目内容
如图，质量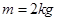
的物体静止于水平地面的A处，A、B间距L=20m。用大小为30N，沿水平方向的外力拉此物体，经
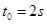拉至B处。(已知
，
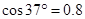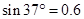。取
)
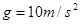(1)求物体与地面间的动摩擦因数μ；
(2)用大小为30N，与水平方向成37°的力斜向上拉此物体，使物体从A处由静止开始运动并能到达B处，求该力作用的最短时间t。
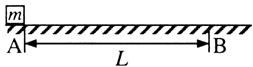
【答案】
(1) 
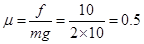(2)1.03s
【解析】(1)物体做匀加速运动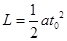 
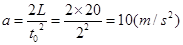(1分)
∴
（1分）
由牛顿第二定律
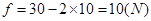（1分）
(1分)
所以 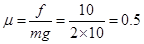(1分)
(2)设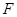
作用的最短时间为
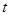，小车先以大小为
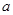的加速度匀加速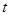秒，撤去外力后，以大小为
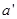，的加速度匀减速
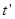秒到达B处，速度恰为0，由牛顿定律
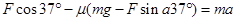(2分)
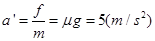（1分）
由于匀加速阶段的末速度即为匀减速阶段的初速度，因此有
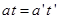（1分）
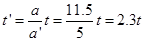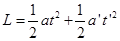（1分）
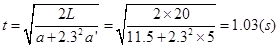（1分）
∴
（1分）
本题考查牛顿第二定律的应用，因为物体做匀加速运动，由位移与时间的关系可求得加速度大小，在该过程中由拉力和摩擦力提供加速度，由牛顿第二定律可求得摩擦力大小，从而求得动摩擦因数的值，拉力作用时间最短的情况是，在施加拉力过程中物体向右匀加速运动，撤去拉力F后向右匀减速运动，直到运动到B点时速度减小到零，先求得两个过程的加速度大小，中间的速度是最大值，根据平均速度等于初速度与末速度和的一半可知，两个过程的平均速度相同，由位移之和为L可求得运动时间
练习册系列答案
一线名师提优试卷系列答案
相关题目
的物体静止于水平地面的A处，A、B间距L=20m。用大小为30N，沿水平方向的外力拉此物体，经
拉至B处。(已知
，
。取
)
的物体静止于水平地面的A处，A、B间距L=20m。用大小为30N，沿水平方向的外力拉此物体，经
拉至B处。(已知
，
。取
)
的物体静止于水平地面的A处，A、B间距L=20m。用大小为30N，
拉至B处。(已知
，
。取
)
的物体静止于水平地面的A处，A、B间距L=20m。用大小为30N，沿水平方向的外力拉此物体，经
拉至B处。(已知
，
。取
)
的物体静止于水平地面的A处，A、B间距L=20m。用大小为30N，
拉至B处。(已知
，
。取
)